Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A và vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
7 tháng 10 2018
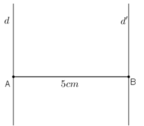
Giả sử đường thẳng d và d’ cắt nhau tại O.
Khi đó qua điểm O ta vẽ được hai đường thẳng phân biệt (d và d’) cùng vuông góc với đường thẳng a (Vô lý).
Vậy đường thẳng d và d’ không cắt nhau.

12 tháng 6 2017
Vì \(d\perp a\) tại A
\(d'\perp a\) tại B
=> d // d'
Vậy 2 đường thẳng d, d' không cắt nhau .

24 tháng 6 2019
Bài làm
Vì d vuông góc với a tại A
d' vuông góc với a tại B
=>d // d'
Vậy 2 đường thẳng d và d' không cắt nhau.
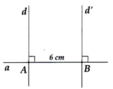
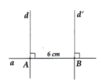
Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
Vì a \( \bot \) d, mà a’ \( \bot \) d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \) a, A \( \in \) a'
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d.