Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác c và d vuông góc với a. Chứng minh rằng:
a) a // b; b) c // d; c) b\( \bot \)d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.

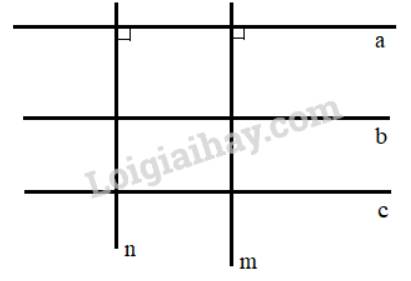
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m

Vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc đồng vị bằng nhau nên a // b (Dấu hiệu nhận biết 2 đường thẳng song song)
a) Vì \(c \bot a;c \bot b \Rightarrow a//b\) ( hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
b) Vì \(a \bot c;a \bot d \Rightarrow c//d\)( hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
c) Vì \(b \bot c;c//d \Rightarrow b \bot d\) ( đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia)