cho tam giác ABC các đường tuyến BD, CE cắt nhau tại G. Vẽ M, N sao cho D là trung điểm GM, E là trung điểm GM. Chứng minh rằng: tứ giác BNMC là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 3 2017
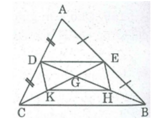
Tam giác ABC có hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm tam giác ABC.
Ta có: GD = 1/2 GB (tính chất đường trung tuyến của tam giác)
GH = 1/2 GB (gt)
Suy ra: GD = GH
GE = 1/2 GC (tính chất đường trung tuyến của tam giác)
GK = 1/2 GC
Suy ra GE = GK
Tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
21 tháng 7 2023
Xét ΔABC có
BD,CE là trung tuyến
BD cắt CE tại G
=>G là trọng tâm
=>BG=2GD và CG=2GE
=>BG=GH và CG=GI
=>G là trung điểm chung của CI và BH
=>BIHC là hình bình hành
29 tháng 4 2018
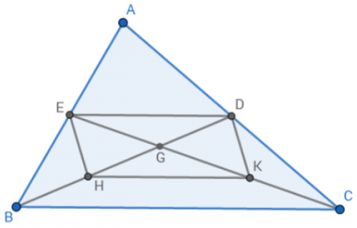
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi
9 tháng 8 2022
Bài 1:
a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
DO dó: ED là đường trung bình
=>ED//BC và ED=BC/2
Xét ΔGBC có
M,N lần lượt là trug điểm của GB và GC
nênMN là đường trung bình
=>MN//BC và MN=BC/2
Xét ΔGMN có
I là trung điểm của GM
K là trung điểm của GN
Do đó: IK là đường trung bình
=>IK//MN và IK=MN/2
=>IK//ED và IK=BC/4
Xét tứ giác IKDE có DE//IK
nên IKDE là hình thang
Xét ΔACE và ΔABD có
AC=AB
góc A chung
AE=AD
Do đó: ΔACE=ΔABD
Suy ra: CE=BD
Xét ΔEBC và ΔDCB có
EB=DC
EC=BD
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: góc GBC=góc GCB
hay ΔGBC cân tại G
=>GB=GC
=>GD=GE
GI=1/4GB
GK=1/4GC
mà GB=GC
nên GI=GK
=>ID=EK
=>EDKI là hình thang cân
b: DE=BC/2=5cm
IK=1/4BC=2,5cm
=>DE+IK=7,5cm