Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Nếu a \( \in \) Z thì a \( \in \) R
b) Nếu a \( \in \) Q thì a \( \in \) R
c) Nếu a \( \in \) R thì a \( \in \) Z
d) Nếu a \( \in \) R thì a \( \notin \) Q
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Nếu \(a \in \mathbb{N}\) thì \(a \in \mathbb{Q}\) => Đúng
b) Nếu \(a \in \mathbb{Z}\) thì \(a \in \mathbb{Q}\) => Đúng
c) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{N}\) => Sai. Vì a là số hữu tỉ thì chưa chắc a là số tự nhiên.
d) Nếu \(a \in \mathbb{Q}\) thì \(a \in \mathbb{Z}\) => Sai. Vì a là số hữu tỉ thì chưa chắc a là số nguyên.
e) Nếu \(a \in \mathbb{N}\) thì \(a \notin \mathbb{Q}\) => Sai. Vì các số tự nhiên là các số hữu tỉ
g) Nếu \(a \in \mathbb{Z}\) thì \(a \notin \mathbb{Q}\) => Sai. Vì các số nguyên là các số hữu tỉ
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) \(\sqrt 3 \in \mathbb{Q}\) sai.
Sửa lại: \(\sqrt 3 \notin \mathbb{Q}\)
b) \(\sqrt 3 \in \mathbb{R}\) đúng.
c) \(\frac{2}{3} \notin \mathbb{R}\) sai.
Sửa lại: \(\frac{2}{3} \in \mathbb{R}\)
d) \( - 9 \in \mathbb{R}\) đúng.
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
Phát biểu a : Đúng, vì \( - 4\) là số nguyên âm nên nó là số nguyên.
Phát biểu b: Đúng, vì 5 là số nguyên dương nên nó là số nguyên.
Phát biểu c: Đúng, vì 0 là số nguyên.
Phát biểu d: Sai, vì \( - 8\) là số nguyên âm, không phải là số tự nhiên.
Phát biểu e: Đúng, vì 6 là số tự nhiên.
Phát biểu f: Đúng, vì 0 là số tự nhiên.
24 tháng 9 2023
Tham khảo:
a)
Mệnh đề P có dạng \(R \Rightarrow T\)với R: “Hai tam giác bằng nhau” và T: “Diện tích của hai tam giác bằng nhau”
Giả thiết là mệnh đề R: “Hai tam giác bằng nhau”
Kết luận là mệnh đề T: “Diện tích của hai tam giác bằng nhau”
Mệnh đề Q có dạng \(A \Rightarrow B\)với A: “\(a < b\)” và B: “\(a + c < b + c\)”
Giả thiết là mệnh đề A: “\(a < b\)”
Kết luận là mệnh đề B: “\(a + c < b + c\)”
b)
+) Mệnh đề P có thể phát biểu lại như sau:
Hai tam giác bằng nhau là điều kiện đủ để có diện tích của chúng bằng nhau.
Diện tích của hai tam giác bằng nhau là điều kiện cần để hai tam giác bằng nhau.
+) Mệnh đề Q có thể phát biểu lại như sau:
\(a < b\) là điều kiện đủ để có \(a + c < b + c\).
\(a + c < b + c\)là điều kiện cần để có \(a < b\).
c)
Mệnh đề đảo của mệnh đề P có dạng \(T \Rightarrow R\), phát biểu là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.
Mệnh đề này sai nên không là định lí.
Chẳng hạn: Tam giác ABC và tam giác DEF, có diện tích bằng nhau nhưng hai tam giác không bằng nhau.
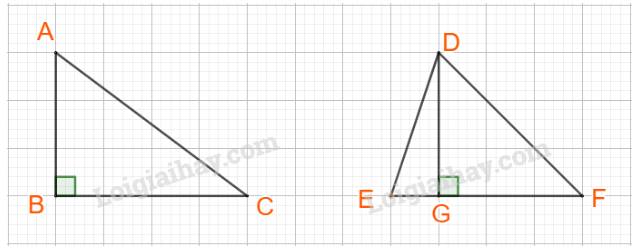
Mệnh đề đảo của mệnh đề Q có dạng \(B \Rightarrow A\), phát biểu là: “Nếu \(a + c < b + c\)thì \(a < b\)”.
Mệnh đề này đúng nên nó cũng là định lí.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Phương trình \({x^2} - 2x - 3 = 0\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 3\)
Có \(a = 1 > 0\) nên
\(f\left( x \right) = {x^2} - 2x - 3 > 0\) khi và chỉ khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
=> Phát biểu a) đúng.
\(f\left( x \right) = {x^2} - 2x - 3 < 0\) khi và chỉ khi \(x \in \left( { - 1;3} \right)\)
=> Phát biểu b) sai vì khi x=-1 hoặc x=3 thì \({x^2} - 2x - 3 = 0\) (không nhỏ hơn 0).
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
\(a)\sqrt 2 \approx 1,1412... \in I;\,\,\,\,\,b)\sqrt 9 = 3 \notin I;\,\,\,\,c)\,\pi \approx 3,141... \in I;\,\,\,\,\,d)\sqrt 4 = 2 \in \mathbb{Q}\)
Vậy các phát biểu a,c,d đúng.
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
a) Đúng vì 9 là số tự nhiên
b) Sai vì \( - 6\) là số nguyên âm, không phải là số tự nhiên.
c) Đúng vì \( - 3\) là số nguyên âm nên nó là số nguyên.
d) Đúng vì 0 là số nguyên
e) Đúng vì số 5 là số nguyên dương nên nó là số nguyên.
g) Đúng vì 20 là số tự nhiên.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Mệnh đề trên có dạng “P nếu và chỉ nếu Q”, là một mệnh đề tương đương với P: “\(x \in \mathbb{Z}\)” và Q: “\(x + 1 \in \mathbb{Z}\)” (\(x \in \mathbb{R}\))
Phát biểu:
“\(\forall x \in \mathbb{R},x \in \mathbb{Z}\) là điều kiện cần và đủ để có \(x + 1 \in \mathbb{Z}\)”
Hoặc “\(\forall x \in \mathbb{R},x + 1 \in \mathbb{Z}\) là điều kiện cần và đủ để có \(x \in \mathbb{Z}\)”
a) Đúng vì 1 số nguyên cũng là số thực
b) Đúng vì 1 số hữu tỉ cũng là số thực
c) Sai vì 1 số thực có thể không là số nguyên. Chẳng hạn, số \(0,2 \in R\) nhưng \(0,2 \notin Z\)
d) Sai vì 1 số thực có thể là số hữu tỉ hoặc không là số hữu tỉ. Chẳng hạn \(0,2 \in R\) và \(0,2 \in Q\)
a: Đúng
b: Đúng
c: Sai
d: Sai