Cho góc ^xOy=40o. Vẽ góc ^xOt kề bù với ^xOy. Vẽ góc ^zOt=70o sao cho tia Oz nằm giữa hai tia Ox và Ot. Gọi Oh là tia phân giác góc ^xOy.
Đường thẳng chứa tia Oh và đường thẳng chứa tia Oz có vuông góc với nhau không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VH
1
Những câu hỏi liên quan
VH
12 tháng 7 2017
Mình không hiểu sao lại giải như vậy.
Tại sao lại tia Ox là tia phân giác của góc xOt.
Bạn nào hiểu thì giúp mình ở phần trả lời.Mình cảm ơn rất nhiều!:D
CM
24 tháng 11 2018
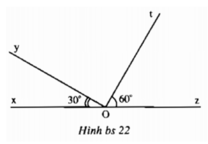
Xem hình bs 22. Rõ ràng hai đường thẳng Ot và Oy cắt nhau tại điểm O. Do góc xOy và góc yOz là hai góc kề bù nên:
∠yOz = 180° - ∠yOx = 150°.
Vì tia Ot nằm giữa hai tia Oz và Oy nên ∠yOt + ∠tOz = ∠yOz, suy ra
∠yOt = ∠yOz - ∠tOz = 150° - 60° = 90°.
T
20 tháng 8 2016
có góc xOy+ góc yOz = 180 độ ( 2 góc kề bù)
mà góc xOy = 30 độ (gt)
=> góc yOz=180 độ - 30 độ = 150 độ
Có góc zOt + góc tOy = góc yOz
mà góc yOz = 150 độ (cmt)
góc zOt= 60 độ (gt)
=> 60 độ + góc tOy= 150 độ
=> góc tOy = 150độ - 60 độ = 90 độ
=> Ot vuông góc vs Oy
vậy đường thẳng chứa tia Ot và đường thẳng chứa tia Oy vuông góc vs nhau
Vì Oh là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\) \(\widehat{xOh}\) = \(\widehat{hOy}\) \(\frac{\widehat{xOy}}{2}\) = \(\frac{\widehat{40^0}}{2}\) = 20*
\(\Rightarrow\) \(\widehat{hOy}\) + \(\widehat{yOz}\) = \(\frac{\widehat{yOz}}{2}\) + \(\frac{\widehat{yOt}}{2}\)
\(\Rightarrow\) \(\widehat{hOy}\) + \(\widehat{zOy}\) = \(\frac{\widehat{yOz}+\widehat{yOt}}{2}\)
\(\Rightarrow\) \(\widehat{hOy}\) + \(\widehat{yOz}\) = \(\frac{180^0}{2}\) = 90* ( Vì \(\widehat{xOy}\) và \(\widehat{yOt}\) là 2 góc kề bù )
hay \(\widehat{hOz}\) = 90*
Vậy Oh vuông góc với Oz