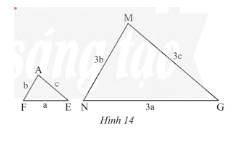
a) Tam giác \(AFE\) và \(MNG\) ở Hình 14 có đồng dạng với nhau không? Vì sao?
b) Biết tam giác \(AFE\) có chu vi bằng 15 cm. Tính chu vi tam giác MNG.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 6 2022
a: Xét ΔAFE và ΔMNG có
AF/MN=AE/MG=FE/NG
nên ΔAFE\(\sim\)ΔMNG
b: \(\dfrac{C_{AFE}}{C_{MNG}}=\dfrac{1}{3}\)
nên \(C_{MNG}=45\left(cm\right)\)
CM
21 tháng 3 2018
a) Ta có:
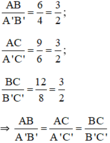
⇒ ΔABC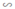 
ΔA’B’C’ (c.c.c).
b) Ta có:
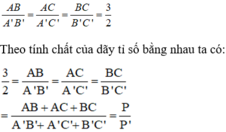
Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là 3/2.
19 tháng 4 2020
a, 2 tam giác đồng dạng
CM:
xét tam giác ta có: \(2x+3x+4x=56\)(\(x\)là hệ số sao cho \(2x;3x;4x\)là ba cạnh của tam giác ABC)
=) \(x=6\)
tỉ lệ cạnh thì cậu chứng minh đc 2 tam giác đồng dạng nhé
b,vì hai tam đồng dạng nên
\(\widehat{ABC}=\widehat{DEF}=45^O\)
\(\widehat{BAC}=\widehat{EDF}=105^O\)
tổng 3 góc trong tam giác =180o
thì tính đc \(\widehat{ACB}=\widehat{DFE}=30^O\)
19 tháng 4 2020
sao khi ra x=6 nhân vào 2x=2.6=12=AB
3x=3.6=18=AC
BC=4x=4.6=24
tỉ lệ cạnh \(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}\)
hay \(\frac{12}{3}=\frac{18}{4,5}=\frac{24}{6}\)
8 tháng 1
a:
MC+MB=BC
=>BC=2MB+MB=3MB
=>\(\dfrac{CM}{CB}=\dfrac{2MB}{3MB}=\dfrac{2}{3}\)
Xét ΔCME và ΔCBA có
\(\widehat{CME}=\widehat{CBA}\)(hai góc đồng vị, ME//AB)
\(\widehat{C}\) chung
Do đó: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{CM}{CB}=\dfrac{CE}{CA}=\dfrac{ME}{BA}=\dfrac{2}{3}\)
b: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}=\dfrac{2}{3}\)
=>\(C_{CME}=\dfrac{2}{3}\cdot24=16\left(cm^2\right)\)
VT
18 tháng 4 2020
6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)
a) Ta có:
\(\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3}\)
Xét tam giác \(AFE\) và tam giác \(MNG\) có:
\(\frac{{AF}}{{MN}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{1}{3} \Rightarrow \frac{{AF}}{{MN}} = \frac{{AE}}{{MG}} = \frac{{EF}}{{NG}}\)
Do đó, \(\Delta AFE\backsim\Delta MNG\) (c.c.c)
b) Tỉ số đồng dạng của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\).
Do đó, tỉ số chu vi của của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\) (tính chất)
Do đó, chu vi tam giác \(MNG\) là: \(15.3 = 45cm\)
Vậy chu vi tam giác \(MNG\) là 45 cm.