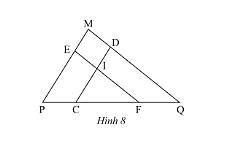
Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
14 tháng 9 2023
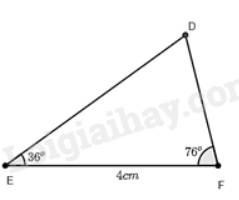
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
QT
1
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Do \(ABCD\) là hình bình hành nên \(BC//AD \Rightarrow EB//AD\)
Xét tam giác \(IDA\) có
\(EB//AD;EB\) cắt \(AI;ID\) tại \(B;E\).
Do đó, \(\Delta IEB\backsim\Delta IDA\) (định lí)
b) Ta có: \(\Delta IEB\backsim\Delta IDA \Rightarrow \frac{{IB}}{{IA}} = \frac{{BE}}{{DA}}\) (hai cặp cạnh tương ứng tỉ lệ).
Mà \(CB = AD;CB = 3BE \Rightarrow AD = 3BE;AI = 9\) nên ta có:
\(\frac{{IB}}{9} = \frac{{BE}}{{3BE}} = \frac{1}{3} \Rightarrow IB = \frac{{9.1}}{3} = 3\).
Vậy \(IB = 3cm.\)
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(ABC\) ta có:
\(DE//BC\) và \(D,E\) cắt \(AB;AC\) tại \(D;E\).
Do đó, \(\Delta ADE\backsim\Delta ABC\) (định lí)
b) Vì \(\Delta ADE\backsim\Delta ABC\) nên \(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\) (cách cặp cạnh tương ứng có cùng tỉ lệ).
Thay số, \(\frac{{16}}{{30}} = \frac{{22}}{{BC}} \Rightarrow BC = \frac{{22.30}}{{16}} = 41,25\)
Vậy \(BC = 41,25m\).
QT
1
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(ABE\) có:
\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).
Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)
b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số ta được:
\(\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)
Vậy \(x = 8\).
4 tháng 3 2023
a: Xét ΔHAB vuông tại Hvà ΔADB vuông tại A có
góc ABD chung
=>ΔHAB đồng dạng với ΔADB
Xét ΔHDA vuông tại H và ΔADB vuông tại A có
góc ADB chung
=>ΔHDA đồng dạng với ΔADB
=>ΔHAB đồng dạng với ΔHDA
Xét ΔHAB vuông tại H và ΔCBD vuông tại C có
góc HBA=góc CDB
=>ΔHAB đồng dạng với ΔCBD
b: Xét ΔABD vuông tại A có AH là đường cao
nên BH*BD=BA^2=CD^2
c: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
BH=8^2/10=6,4cm
HD=10-6,4=3,6cm
15 tháng 9 2023
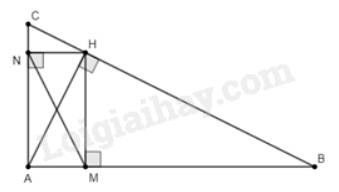
a) Xét \(\Delta AMH\) và \(\Delta AHB\) có:
\(\widehat {HAM}\) chung (do \(\widehat {HAM}\) cũng là \(\widehat {HAB}\))
\(\widehat {AMH} = \widehat {AHB} = 90^\circ \) (do \(HM \bot AB\) và \(AH\) là đường cao)
Do đó, \(\Delta AMH\backsim\Delta AHB\) (g.g).
b) Vì \(\Delta AMH\backsim\Delta AHB\) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra \(AM.AB = A{H^2}\) (1)
- Xét \(\Delta ANH\) và \(\Delta AHC\) có:
\(\widehat {HAN}\) chung (do \(\widehat {HAN}\) cũng là \(\widehat {HAC}\))
\(\widehat {ANH} = \widehat {AHC} = 90^\circ \) (do \(HN \bot AC\) và \(AH\) là đường cao)
Do đó, \(\Delta ANH\backsim\Delta AHC\) (g.g).
Vì \(\Delta ANH\backsim\Delta AHC\) nên \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra \(AN.AC = A{H^2}\) (2)
Từ (1) và (2) suy ra, \(AM.AB = AN.AC\)(điều phải chứng minh).
c) Từ câu b ta có:
\(AM.AB = AN.AC \Rightarrow \frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\) (tỉ lệ thức)
Xét \(\Delta ANM\)và \(\Delta ABC\) ta có:
\(\widehat A\) chung
\(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\) (chứng minh trên)
Do đó, \(\Delta ANM\backsim\Delta ABC\)(c.g.c)
d) Áp dụng định lí Py- ta – go cho tam giác \(ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{B^2} + A{C^2} = {9^2} + {12^2} = 225 \Rightarrow BC = 15cm\)
Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\)
\( \Rightarrow AH.BC = AB.AC\)
\( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{9.12}}{{15}} = 7,2cm\).
Ta có: \(A{H^2} = AM.AB = AM.9 = 7,{2^2} \Rightarrow AM = \frac{{7,{2^2}}}{9} = 5,76cm\)
\(A{H^2} = AN.AC = AN.12 = 7,{2^2} \Rightarrow AN = \frac{{7,{2^2}}}{{12}}4,32cm\).
Diện tích tam giác vuông \(AMN\) là:
\({S_{AMN}} = \frac{1}{2}AM.AN = \frac{1}{2}.5,76.4,32 = 12,4416c{m^2}\).
Vậy diện tích tam giác \(AMN\) là 12,4416cm2.
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).