Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2017
C1;
Sơ đồ mạch điện hình 19.3:
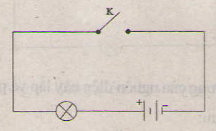
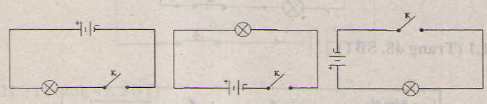
C2:
Các bn mắc mạch điện theo một trong các sơ đồ của câu C2 để kiểm tra
Chúc bn hok tốt
TL
Trịnh Long
CTVVIP
22 tháng 6 2021
F1 : AaBbDD x AabbDd
Xét từng cặp tính trạng :
F1 : Aa x Aa -> 1/4 AA : 2/4 Aa : 1/4 aa ( 3A- : 1aa )
F1 : Bb x bb -> 1/2 Bb : 1/2 bb (1/2 B- : 1bb )
F1 : DD x Dd -> 1/2 DD : 1/2 Dd 100% D-
TLKG : 1/16 AABbDD : 1/16 AABbDd : 1/16 AAbbDD : 1/16 AAbbDd : 2/16 AaBbDD : 2/16 AaBbDd : 2/16 AabbDD : 2/16 AabbDd : 1/16 aaBbDD : 1/16 aaBbDd : 1/16 aabbDD : 1/16 aabbDd
TLKH : dựa vào TLKG
Tỉ lệ KH A-B-D- : 3/4 . 1/2 . 1 = 3/8
Tỉ lệ KG AaBbDd : 2/4 . 1/2 . 1/2 = 1/8
DT
15 tháng 2 2021
Ta thực hiện phép lai riêng rẽ từng cặp tính trạng
Aa x Aa ---> 1/4AA:1/2Aa:1/4aa= 3/4 A_ :1/4aa
Bb x bb ----> 1/2Bb:1/2bb
Dd x Dd ----> 1/4DD:1/2Dd:1/4dd=3/4D_:1/4dd
Ee x Ee ----> 1/4EE:1/2Ee:1/4ee=3/4E_:1/4ee
* Tỉ lệ kiểu gen AaBbDdEe =1/2 x 1/2 x 1/2 x 1/2 = 1/16
* Tỉ lệ kiểu hình A-B-ddee = 3/4 x 1/2 x 1/4 x 1/4 =3/128
* Tỉ lệ kiểu hình mang 3 tính trạng trội.
Th1: A_B_D_ee = aaB_D_E_=A_B_ddE_=3/4x 1/2 x 3/4 x 1/4=9/128
Th2: A_bbD_E_= 3/4 x 1/2 x 3/4 x 3/4 = 27/128
=>Kq là: 9/128 x 3 + 27/128 = 27/64
TL
Trịnh Long
CTVVIP
23 tháng 6 2021
F1 : AaBbDD x AabbDd
Xét từng cặp tính trạng :
F1 : Aa x Aa -> 1/4 AA : 2/4 Aa : 1/4 aa ( 3A- : 1aa )
F1 : Bb x bb -> 1/2 Bb : 1/2 bb (1/2 B- : 1bb )
F1 : DD x Dd -> 1/2 DD : 1/2 Dd 100% D-
TLKG : 1/16 AABbDD : 1/16 AABbDd : 1/16 AAbbDD : 1/16 AAbbDd : 2/16 AaBbDD : 2/16 AaBbDd : 2/16 AabbDD : 2/16 AabbDd : 1/16 aaBbDD : 1/16 aaBbDd : 1/16 aabbDD : 1/16 aabbDd
TLKH : 3/8 A-B-D- : 3/8 A-bbD- : 1/8 aaB-D- : 1/8 aabbD-.
LM
Lê Minh Vũ
CTVHS
VIP
26 tháng 9 2021
Bài 1:
Ta có: \(15m=1500cm\)\(;\) \(10m=1000cm\)
Chiều dài của hình chữ nhật trên bản đồ là :
\(1500\div500=3\left(cm\right)\)
Chiều rộng của hình chữ nhật trên bản đồ là:
\(1000\div500=2\left(cm\right)\)
Bài 2:
Quãng đường Thành phố Hồ Chí Minh – Quy Nhơn dài là:
\(27\times2500000=67500000\left(cm\right)\)
Đổi: \(67500000cm=675km\)
Đáp số: \(675km\)
LM
Lê Minh Vũ
CTVHS
VIP
26 tháng 9 2021
Bài 3:
Thời gian ngủ của Nam là:
\(\frac{5}{8}-\frac{1}{4}=\frac{3}{8}\) (ngày)
Đáp số: \(\frac{3}{8}\)ngày
Bài 4:
Diện tích cây xanh bằng:
\(\frac{6}{7}-\frac{2}{5}=\frac{16}{35}\) (diện tích công viên)
Đáp số: \(\frac{16}{35}\)diện tích công viên
NV
Nguyễn Việt Dũng
CTVVIP
23 tháng 10 2023
Qui ước:
P: Q AaBbCcDdEe (bố)
x: ở aaBbccDdee (mẹ)
a. Số loại kiểu gen:
Kiểu gen của bố (P) là AaBbCcDdEe và kiểu gen của mẹ (x) là aaBbccDdee. Do đó, số loại kiểu gen là 2.
Số loại kiểu hình:
Kiểu hình của bố (P) là phản ánh các gen của mình, nên cũng là AaBbCcDdEe. Kiểu hình của mẹ (x) là phản ánh các gen của mình, nên cũng là aaBbccDdee.
Vì vậy, số loại kiểu hình cũng là 2 (AaBbCcDdEe và aaBbccDdee).
b. Tỉ lệ đời con có kiểu hình giống bố:
Tỉ lệ đời con có kiểu hình giống bố (AaBbCcDdEe) sẽ là 0, vì mẹ không có bất kỳ gen nào giống với bố. Do đó, tỉ lệ này sẽ là 0%.
c. Tỉ lệ đời con mang kiểu hình ít nhất một tỉnh trạng lặn:
Để tính tỉ lệ này, chúng ta cần tính tỉ lệ các đời con không có kiểu hình lặn (aaBbccDdee). Điều này có thể được tính bằng cách tính tỉ lệ đời con có kiểu hình lặn và sau đó trừ tỉ lệ đó từ 100%.
Kiểu hình lặn chỉ xuất hiện khi cả hai bố mẹ đều mang ít nhất một gen lặn. Bố không mang gen lặn, vì vậy chỉ có mẹ mang gen lặn.
Tỉ lệ đời con có kiểu hình lặn từ mẹ là 1/4 (vì con có thể nhận được gen aa từ mẹ). Tỉ lệ đời con không có kiểu hình lặn từ mẹ là 1 - 1/4 = 3/4.
Tổng tỉ lệ đời con không có kiểu hình lặn sẽ là:
Tỉ lệ từ bố (0) * Tỉ lệ từ mẹ (3/4) = 0
Vì vậy, tỉ lệ đời con mang ít nhất một tỉnh trạng lặn là 100% - 0% = 100%.
Ta có:
\(AD = 1,5m;AE = 3m;BD = 3m;EC = 6m;\)
\(AB = AD + DB = 1,5 + 3 = 4,5m;AC = AE + EC = 3 + 6 = 9m\)
Ta có:
\(\frac{{AD}}{{BD}} = \frac{{1,5}}{3} = \frac{1}{2};\frac{{AE}}{{EC}} = \frac{3}{6} = \frac{1}{2}\). Do đó, \(AD\) và \(BD\) tỉ lệ với \(AE\) và \(EC\).
\(\frac{{AD}}{{AB}} = \frac{{1,5}}{{4,5}} = \frac{1}{3};\frac{{AE}}{{AC}} = \frac{3}{9} = \frac{1}{3}\). Do đó, \(AD\) và \(AB\) tỉ lệ với \(AE\) và \(AC\).
\(\frac{{AB}}{{BD}} = \frac{{4,5}}{3} = \frac{3}{2};\frac{{AC}}{{EC}} = \frac{9}{6} = \frac{3}{2}\). Do đó, \(AB\) và \(BD\) tỉ lệ với \(AC\) và \(EC\).