a) Vẽ đồ thị của hàm số \(y = x\) và \(y = x + 2\) trên cùng một mặt phẳng tọa độ.
b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
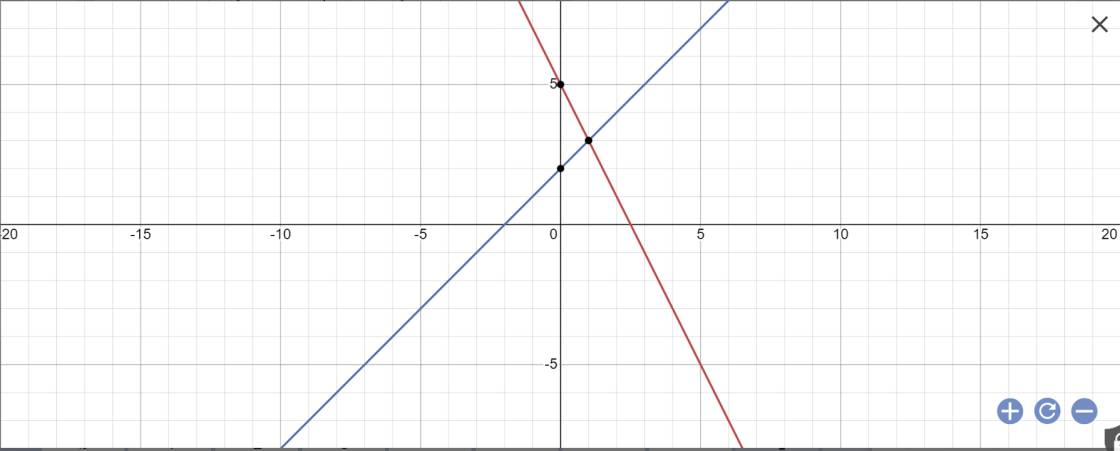
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6

b: Tọa độ điểm C là:
\(\left\{{}\begin{matrix}x-3=-2x+3\\y=x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)

a: 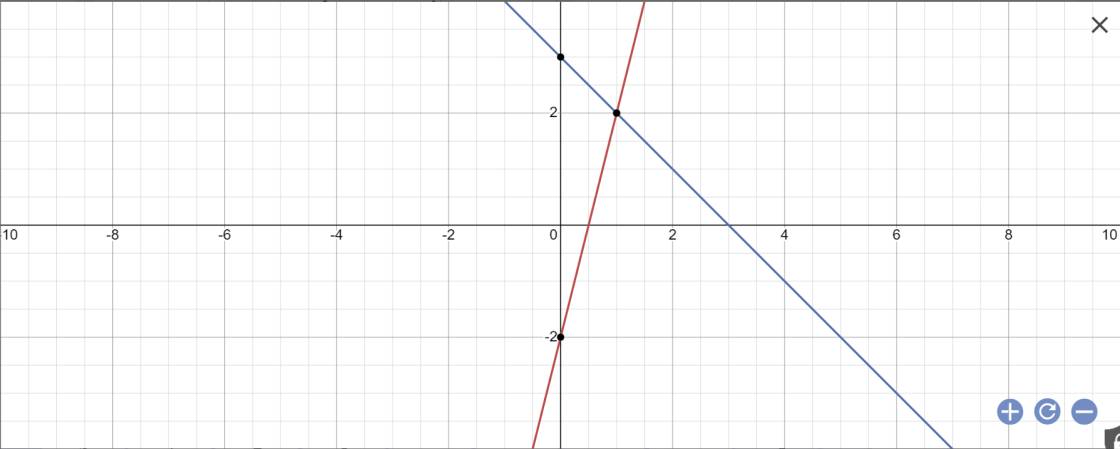
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)

Lời giải:
a.
Đồ thị màu xanh lá: $y=\frac{1}{2}x+1$
Đồ thị màu xanh dương: $y=-x-1$
b.
Ta có:
$\tan \alpha=\frac{1}{2}\Rightarrow \alpha=26,57^0$
$\tan \beta = -1\Rightarrow \beta=135^0$

\(b,\) PT giao Ox tại A và B: \(\left\{{}\begin{matrix}x+2=0\Rightarrow x=-2\Rightarrow A\left(-2;0\right)\\-x+4=0\Rightarrow x=4\Rightarrow B\left(4;0\right)\end{matrix}\right.\)
PT hoành độ giao điểm: \(x+2=-x+4\Rightarrow x=1\Rightarrow y=3\Rightarrow C\left(1;3\right)\)
\(c,OA=\left|x_A\right|=2;OB=\left|x_B\right|=4\\ \Rightarrow AB=OA+OB=6\left(cm\right)\\ \left\{{}\begin{matrix}AC=\sqrt{\left(-2-1\right)^2+3^2}=2\sqrt{3}\left(cm\right)\\BC=\sqrt{\left(4-1\right)^2+3^2}=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Kẻ đường cao CH của ABC
\(\Rightarrow CH=\left|y_C\right|=3\left(cm\right)\)
\(\Rightarrow P_{ABC}=AB+BC+CA=4\sqrt{3}+6\left(cm\right)\\ S_{ABC}=\dfrac{1}{2}CH\cdot AB=\dfrac{1}{2}\cdot3\cdot6=9\left(cm^2\right)\)

Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).
Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).

b. PTHĐGĐ của hai hàm số:
\(x+2=-2x+1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)
Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)

a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
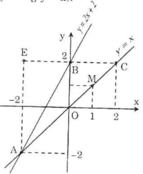
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
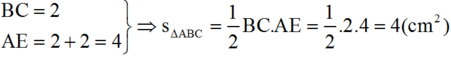
a)
+) y = 2x + 2
Cho x = 0 => y = 2
=> ( 0 ; 2 )
y = 0 => x = -1
=> ( -1 ; 0 )
- Đồ thị hàm số y = x đi qua 2 điểm có tọa độ ( 0 ; 0 )
- Đồ thị hàm số y = 2x + 2 đi qua 2 điểm có tọa độ ( 0 ; 2 ) và ( -1 ; 0 )
b) Hoành độ điểm A là nghiệm của PT sau :
x = 2x + 2
<=> 2x - x = -2
<=> x = -2
=> y = -2
Vậy A ( -2 ; -2 )
c) Tung độ điểm C = 2 => hoành độ điểm C là x = 2
=> C ( 2 ; 2 )
Từ A hạ \(AH\perp BC\), ta có : AH = 4cm
BC = 2cm
Vậy : ..............
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.4.2=4\left(cm^2\right)\)

\(b,\text{PT hoành độ giao điểm: }x+2=-2x+1\Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\Leftrightarrow y=\dfrac{5}{3}\Leftrightarrow A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\\ c,\text{Gọi }y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne1\\-\dfrac{1}{3}a+b=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{7}{3}\end{matrix}\right.\\ \Leftrightarrow y=2x+\dfrac{7}{3}\)
a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).