Cho một đoạn thẳng dài AB = 240 m. Vào cùng một thời điểm một xe xuất phát từ A với tốc độ ban đầu 7,2 km/h và chuyển động nhanh dần đều với gia tốc có độ lớn 0,4 m/\(s^{^2}\). Cùng lúc đó một xe khác xuất phát từ B đi về phía A với tốc độ ban đầu 36 km/h và chuyển động chậm dần đều với gia tốc có độ lớn 0,4 m/\(s^2\)
a) Viết phương trình chuyển động của mỗi người
b) Xác định thời điểm và vị trí hai xe gặp nhau



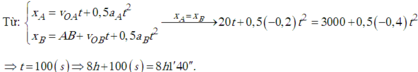
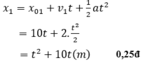
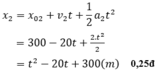
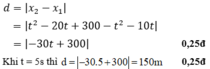
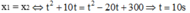 (0,25đ)
(0,25đ)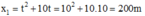 (0,25đ)
(0,25đ)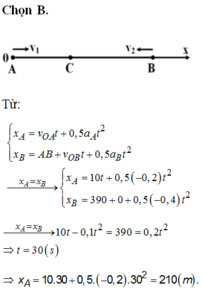

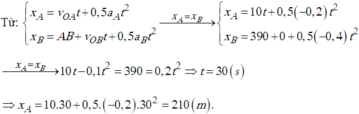
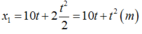
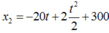
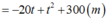
Chọn gốc tọa độ tại A.
Chiều dương từ A đến B.
Gốc thời gian lúc khởi hành.
Lúc \(t_0=0\)
Xe 1 : \(x_{01}=0;v_{01}=+7,2km/h=+2m/s;a_1=+0,4m/s^2\)
Xe 2 : \(x_{02}=240m;v_{02}=-36km/h=-10m/s;a_2=+0,4m/s^2\)
\(a,PTCD\) của 2 xe : \(x=\dfrac{1}{2}at^2+v_0t+x_0\)
Xe 1 : \(x_1=\dfrac{1}{2}.0,4.t^2+2t+0\\ x_1=\dfrac{1}{5}t^2+2t\left(m;s\right)\)
Xe 2 : \(x_2=\dfrac{1}{2}.0,4.t^2+\left(-10\right).t+240\\ x_2=\dfrac{1}{5}t^2-10t+240\left(m;s\right)\)
Vậy phương trình chuyển động của 2 xe lần lượt là \(x_1=\dfrac{1}{5}t^2+2t\left(m;s\right),x_2=\dfrac{1}{5}t^2-10t+240\left(m;s\right)\)
\(b,\) Khi 2 xe gặp nhau thì : \(x_1=x_2\)
\(\Leftrightarrow\dfrac{1}{5}t^2+2t=\dfrac{1}{5}t^2-10t+240\\ \Leftrightarrow t=20\left(s\right)\)
Thay \(t=20\) vào \(x_1=\dfrac{1}{5}.20^2+2.20=120\left(m\right)\)
Vậy 2 xe gặp nhau sau \(20s\) kể từ lúc xuất phát, vị trí gặp nhau cách A \(120m\).