Cho biết Sina=12/13 , tính tana?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tana = 3/4.
=>cota=1/ tana =1:3/4=4/3
sina /cosa =tana
=> sina =tana .cosa =3/4. cosa
lại có sin^2(a)+cos^2(a)=1
<=>9/16cos^2(a)+cos^2=1
<=>25/16cos^2(a)=1
<=>cos^2(a)=16/25
=>[cosa =4/5=>sina =3/5
[cosa =-4/5=> sina =-2/5

a) Có: `1+tan^2a=1/(cos^2a)`
`<=> 1+(3/5)^2=1/(cos^2a)`
`=> cosa=\sqrt10/4`
`=> sina = \sqrt(1-cos^2a) = \sqrt6/4`
b) Có: `sin^2a + cos^2a=1`
`<=> sin^2a + (1/4)^2=1`
`=> sina=\sqrt15/4`
`=> tana = (sina)/(cosa) = \sqrt15`
Má ơi,tính sai:
a)\(\left[{}\begin{matrix}cos\alpha=\dfrac{5\sqrt{34}}{34}\\cos\alpha=\dfrac{-5\sqrt{34}}{34}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}sin\alpha=cos\alpha.tan\alpha=\dfrac{3\sqrt{34}}{34}\\sin\alpha=cos\alpha.tan\alpha=\dfrac{-3\sqrt{34}}{34}\end{matrix}\right.\)
b)\(\left[{}\begin{matrix}sin\alpha=\dfrac{\sqrt{15}}{4}\\sin\alpha=\dfrac{-\sqrt{15}}{4}\end{matrix}\right.\)\(\left[{}\begin{matrix}tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\sqrt{15}\\tatn\alpha=-\sqrt{15}\end{matrix}\right.\)

Ta có tan α . c ot α = 1 ⇒ 12. cot α = 1 ⇔ cot α = 1 12
Lại có 1 sin 2 α = 1 + cot 2 α = 1 + 1 144 = 145 144 ⇔ sin 2 α = 144 145
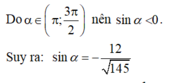
Đáp án D

tana = sina/cosa = 2 => sina = 2cosa
Thay sina = 2cosa vào biểu thức, ta có:
(sina + cosa)/(sina - cosa) = (2cosa + cosa)/(2cosa - cosa) = 3cosa/cosa = 3
Kết luận: (sina + cosa)/(sina - cosa) = 3
P/s: Bài này tui làm rồi
Ai biết làm thì trả lời hộ mình với, cảm ơn rất nhiều ! Xin lỗi vì viết câu trả lời không liên quan, thật lòng xin lỗi !

\(\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}\)

\(sina=\dfrac{12}{13}\\ \Rightarrow cosa=\sqrt{1-\left(\dfrac{12}{13}\right)^2}=\dfrac{5}{13}\\ tana=\dfrac{sina}{cosa}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)