Khẳng định sau đúng hay sai? Vì sao?
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
Khẳng định C là khẳng định sai vì:
Nếu: \(\frac{{x + 1}}{{x - 1}} = \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}}\)
\(\begin{array}{l} \Rightarrow \frac{{x + 1}}{{x - 1}} - \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}} = 0\\ \Rightarrow \frac{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) - \left( {{x^2} + x + 1} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = 0\\ \Rightarrow \frac{{\left( {{x^3} + 1} \right) - \left( {{x^3} - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = \frac{2}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = 0\end{array}\)
\( \Rightarrow \) vô lý
H
9 tháng 9 2023
Khẳng định `A` là đúng vì :
\(\dfrac{\left(x-1\right)^2}{x-2}\\ =\dfrac{\left(x-1\right)^2}{-\left(x-2\right)}\\ =\dfrac{\left(1-x\right)^2}{2-x}\)
`->` Đã là hằng đẳng thức mũ `2` thì `(x-1)^2=(1-x)^2`
NV
Nguyễn Việt Dũng
CTVVIP
9 tháng 9 2023
Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.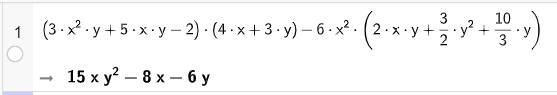
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
Ta có: \(\frac{5}{{2{{\rm{x}}^2}\left( {6{\rm{x}} + y} \right)}} + \frac{3}{{5{\rm{x}}y\left( {6{\rm{x}} + y} \right)}} = \frac{{25y}}{{10{{\rm{x}}^2}y\left( {6{\rm{x}} + y} \right)}} + \frac{{6{\rm{x}}}}{{10{{\rm{x}}^2}y\left( {6{\rm{x}} + y} \right)}} = \frac{{25y + 6{\rm{x}}}}{{10{{\rm{x}}^2}y\left( {6{\rm{x}} + y} \right)}}\)
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
a) Đây là kết luận đúng vì: \( - 6.2{y^2} = - 3y.4y\)
b) Đây là kết luận đúng vì: \(5{\rm{x}}\left( {x + 3} \right) = 5\left( {{x^2} + 3{\rm{x}}} \right) = 5{{\rm{x}}^2} + 15{\rm{x}}\)
c) Đây là kết luận đúng vì: \(3{\rm{x}}\left( {4{\rm{x}} + 1} \right)\left( {1 - 4{\rm{x}}} \right) = 3{\rm{x}}\left( {1 - 16{{\rm{x}}^2}} \right) = - 3{\rm{x}}\left( {16{{\rm{x}}^2} - 1} \right)\)
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right):\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right) = \frac{{ - 3{\rm{x}}}}{{5{\rm{x}}{y^2}}}.\frac{{ - 12{\rm{x}}y}}{{5{y^2}}} = \frac{{36{{\rm{x}}^2}y}}{{25{\rm{x}}{y^4}}}\)
b) \(\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}:\frac{4{{\text{x}}^{2}}+4\text{x}+1}{4{{\text{x}}^{2}}+2\text{x}+1}=\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}.\frac{4{{\text{x}}^{2}}+2\text{x}+1}{4{{\text{x}}^{2}}+4\text{x}+1}\)
\(=\frac{\left( 2\text{x}-1 \right)\left( 2\text{x}+1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right)}{\left( 2\text{x}-1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right){{\left( 2\text{x}+1 \right)}^{2}}}=\frac{1}{2\text{x}+1}\).
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right).\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right) = \frac{{\left( { - 3{\rm{x}}} \right).\left( { - 5{y^2}} \right)}}{{5{\rm{x}}{y^2}.12{\rm{x}}y}} = \frac{1}{{4{\rm{x}}y}}\)
\(b)\frac{{{x^2} - x}}{{2{\rm{x}} + 1}}.\frac{{4{{\rm{x}}^2} - 1}}{{{x^3} - 1}} = \frac{{x\left( {x - 1} \right).\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}{{\left( {2{\rm{x}} + 1} \right).\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{x\left( {2{\rm{x}} - 1} \right)}}{{{x^2} + x + 1}}\)
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
\(\begin{array}{l}a)\frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\left( {\frac{1}{{2{\rm{x}} + 1}} + \frac{1}{{2{\rm{x}} - 1}} + \frac{1}{{1 - 4{{\rm{x}}^2}}}} \right)\\ = \frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\frac{{2{\rm{x}} - 1 + 2{\rm{x}} + 1 - 1}}{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}\\ = \frac{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}{{\left( {4{\rm{x}} - 1} \right)\left( {4{\rm{x + 1}}} \right)}}.\frac{{4{\rm{x}} - 1}}{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}\\ = \frac{1}{{4{\rm{x}} + 1}}\\b)\left( {\frac{{x + y}}{{xy}} - \frac{2}{x}} \right).\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\\ = \frac{{x + y - 2y}}{{xy}}.\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\\ = \frac{{\left( {x - y} \right).{x^3}{y^3}}}{{xy\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{{{x^2}{y^2}}}{{{x^2} + xy + y{}^2}}\end{array}\)
HQ
Hà Quang Minh
Giáo viên
10 tháng 1
a)
\(\begin{array}{l}A = 0,2\left( {5{\rm{x}} - 1} \right) - \dfrac{1}{2}\left( {\dfrac{2}{3}x + 4} \right) + \dfrac{2}{3}\left( {3 - x} \right)\\A = x - 0,2 - \dfrac{1}{3}x - 2 + 2 - \dfrac{2}{3}x\\ = \left( {x - \dfrac{1}{3}x - \dfrac{2}{3}x} \right) + \left( {\dfrac{{ - 1}}{2} - 2 + 2} \right)\\ = - \dfrac{1}{2}\end{array}\)
Vậy \(A = - \dfrac{1}{2}\) không phụ thuộc vào biến x
b)
\(\begin{array}{l}B = \left( {x - 2y} \right)\left( {{x^2} + 2{\rm{x}}y + 4{y^2}} \right) - \left( {{x^3} - 8{y^3} + 10} \right)\\B = \left[ {x - {{\left( {2y} \right)}^3}} \right] - {x^3} + 8{y^3} - 10\\B = {x^3} - 8{y^3} - {x^3} + 8{y^3} - 10 = - 10\end{array}\)
Vậy B = -10 không phụ thuộc vào biến x, y.
c)
\(\begin{array}{l}C = 4{\left( {x + 1} \right)^2} + {\left( {2{\rm{x}} - 1} \right)^2} - 8\left( {x - 1} \right)\left( {x + 1} \right) - 4{\rm{x}}\\{\rm{C = 4}}\left( {{x^2} + 2{\rm{x}} + 1} \right) + \left( {4{{\rm{x}}^2} - 4{\rm{x}} + 1} \right) - 8\left( {{x^2} - 1} \right) - 4{\rm{x}}\\C = 4{{\rm{x}}^2} + 8{\rm{x}} + 4 + 4{{\rm{x}}^2} - 4{\rm{x}} + 1 - 8{{\rm{x}}^2} + 8 - 4{\rm{x}}\\C = \left( {4{{\rm{x}}^2} + 4{{\rm{x}}^2} - 8{{\rm{x}}^2}} \right) + \left( {8{\rm{x}} - 4{\rm{x}} - 4{\rm{x}}} \right) + \left( {4 + 1 + 8} \right)\\C = 13\end{array}\)
Vậy C = 13 không phụ thuộc vào biến x
Khẳng định trên là đúng. Vì nhân cả tử và mẫu của phân thức \(\frac{{2y}}{{3\left( {x - y} \right)}}\) với 15 ta được phân thức
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} \Rightarrow \frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Khẳng định trên là đúng vì :
\(\dfrac{30xy^2\left(x-y\right)}{45xy\left(x-y\right)^2}\\ =\dfrac{30xy^2\left(x-y\right):15xy\left(x-y\right)}{45xy\left(x-y\right)^2:15xy\left(x-y\right)}\\ =\dfrac{2y}{3\left(x-y\right)}\left(dpcm\right)\)