Trong tình huống mở đầu, giả sử vận tốc trung bình của một vận động viên đi xe đạp trên 36 km đường bằng phẳng là x (km/h). Hãy viết biểu thức biểu thị thời gian vận động viên đó hoàn thành chặng leo dốc, chặng xuống dốc, chặng đường bằng phẳng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vận động viên số 1 nha bạn mk làm rồi chắc chắn lun k cho mk nha và mk chúc bạn học tốt!Thank you very much!!!

Tham khảo:
a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ
Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)
Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)
Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)
Như vậy hàm số tính quãng đường s (km) sau t phút là:
\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)
b)
Với \(0 \le t \le 90\) thì \(s = 0,7t\)
Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)
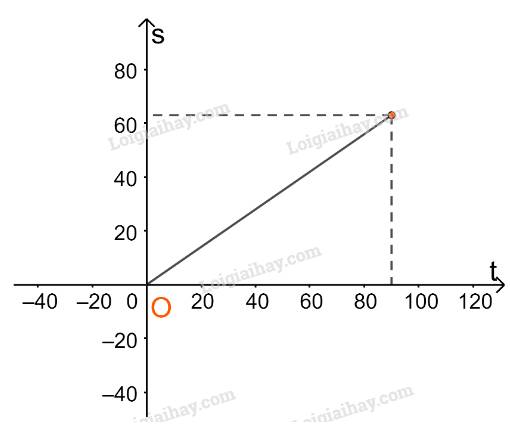
Với \(90 < t \le 105\) thì \(s = 63(km)\)
Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)
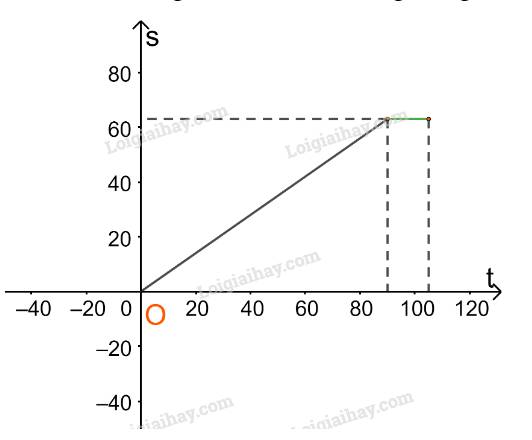
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)
Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)
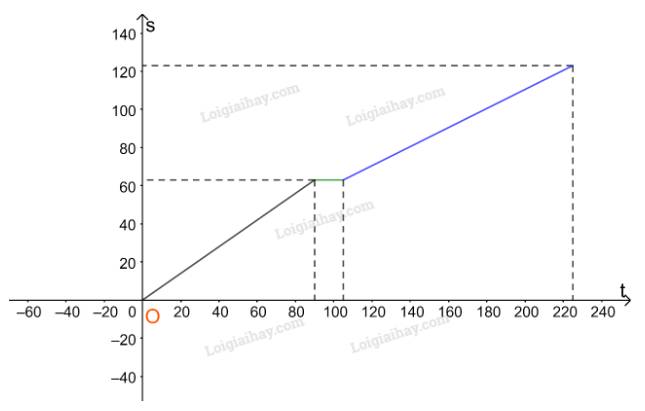
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.

Đổi: \(20ph=\dfrac{1}{3}h\)
a) \(v_1=\dfrac{S_1}{t_1}=\dfrac{15}{\dfrac{1}{3}}=45\left(km/h\right)\)
b) \(S_2=v_2.t_2=15.0,5=7,5\left(km\right)\)
c) \(t_3=\dfrac{S_3}{v_3}=\dfrac{10}{60}=\dfrac{1}{6}\left(h\right)\)
- Thời gian vận động viên đó hoàn thành chặng leo dốc: \(\)\(t = \frac{9}{{x - 5}}\)
- Thời gian vận động viên đó hoàn thành chặng xuống dốc: \(t = \frac{5}{{x + 10}}\)
- Thời gian vận động viên đó hoàn thành chặng đường bằng phẳng: \(t = \frac{{36}}{x}\)