Cho tam giác ABC , \(\widehat{B}=2\widehat{C}\) và \(CB=2AB\) . Tính các góc của tam giác đó .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
G
29 tháng 11 2017
Bạn tham khảo ở đây:
Câu hỏi của Nguyễn Khánh Ngân - Toán lớp 7 - Học toán với OnlineMath
28 tháng 7 2019
Link nek:
Câu hỏi của Nguyễn Khánh Ngân - Toán lớp 7 - Học toán với OnlineMath
Bn tham khảo ở đây nha
~ Rất vui vì giúp đc bn ~
25 tháng 9 2023
Tham khảo:
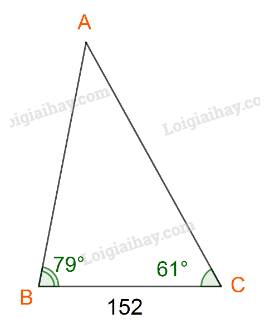
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}\)
Áp dụng định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra:
\(\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{2\sin A}} = \frac{{152}}{{2\sin {{40}^o}}} \approx 118,235\end{array}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)
25 tháng 9 2023
Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
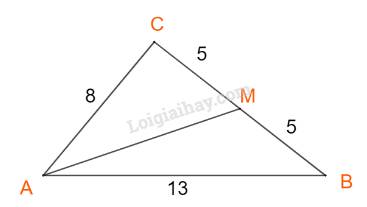
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)
Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)
15 tháng 9 2021
Vì \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}\) nên \(\widehat{A}-2\widehat{B}+\widehat{C}=0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}-2\widehat{B}+\widehat{C}=0^0\left(1\right)\\\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(2\right)\end{matrix}\right.\)
Trừ \(\left(2\right)\) cho \(\left(1\right)\), ta được \(3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)
\(\Rightarrow\widehat{A}+\widehat{C}=120^0\)
Vậy GTLN của \(\widehat{A}\) là \(119^0\) vì \(\widehat{C}>0\)
10 tháng 9 2017
Xin chào đồng loại. À k, fải là xin chào "c - hó" ms đúng tên của pạn chứ nhỉ, bạn "depgiaicogisaidau" thân yêu!
P/s: mai đổi thành "lachocogisaidau" nha!
21 tháng 10 2018
Gọi \(\widehat{A}:\widehat{B}:\widehat{C}\)lần lượt là a,b,c
Do \(\widehat{A}:\widehat{B}:\widehat{C}=3:4:5\)
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}\)
Mà tổng \(\widehat{A}:\widehat{B}:\widehat{C}=180^o\)(tổng 3 góc trong tam giác)
=>\(\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{3}\\\frac{b}{4}\\\frac{c}{5}\end{cases}}=15\)
\(\Rightarrow\hept{\begin{cases}a=45^o\\b=60^o\\c=75^o\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=45^o\\\widehat{B}=60^o\\\widehat{C}=75^o\end{cases}}\)
MÀ \(\Delta ABC=\Delta A'B'C'\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=\widehat{A'}\\\widehat{B}=\widehat{B'}\\\widehat{C}=\widehat{C'}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{A'=45^o}\\\widehat{B'=60^o}\\\widehat{C'}=75^o\end{cases}}\)
21 tháng 10 2018
Đặt: \(\widehat{A}=3x\Rightarrow\hept{\begin{cases}\widehat{B}=4x\\\widehat{C}=5x\end{cases}}\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow3x+4x+5x=180^o\)
\(\Rightarrow x=15\)
\(\Rightarrow\hept{\begin{cases}\widehat{A'}=\widehat{A}=3x=45^o\\\widehat{B}'=\widehat{B}=4x=60^o\\\widehat{C'}=\widehat{C}=75^o\end{cases}}\)
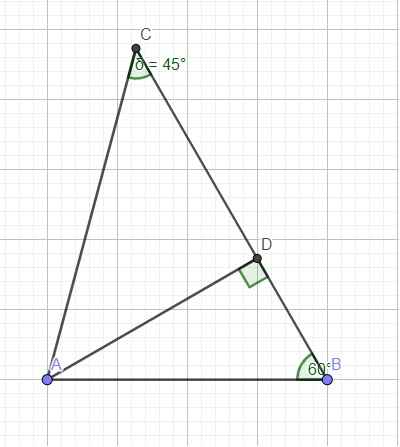
Hình vẽ chỉ mang tính chất minh hoạ thôi nha bạn.
Trên tia đối của AB lấy điểm D sao cho \(BD\text{=}BC\)
Do đó :
Ta có : tam giác BDC cân tại B
\(AD\text{=}DB+AB\text{=}BC+AB\text{=}3AB\)
\(\Rightarrow\widehat{ABC}\text{=}\widehat{BDC}+\widehat{BCD}\text{=}2\widehat{BCD}\)
Mà : \(\widehat{B}\text{=}2\widehat{C}\) nên \(\widehat{B}\text{=}\widehat{DCA}\)
Xét \(\Delta BAC\) và \(\Delta CAD\) có :
\(\widehat{A}:gócchung\)
\(\widehat{B}\text{=}\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\Delta BAC\sim\Delta CAD\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{AC}\text{=}\dfrac{AC}{AD}\) \(\Rightarrow AC^2\text{=}AB.AD\)
Mà \(AD\text{=}3AB\) \(\Rightarrow AC^2\text{=}3AB^2\)
Ta có : \(BC^2\text{=}4AB^2\)
Xét tam giác ABC có : \(AB^2+AC^2\text{=}AB^2+3AB^2\text{=}4AB^2\text{=}BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
Kết hợp với gt của đề bài : \(\Rightarrow\widehat{A}\text{=}90^o;\widehat{C}\text{=}30^o;\widehat{B}\text{=}60^o\).
Cảm ơn.