Cho hình bình hành ABCD, cạnh AB cố định, đường cheó AC=2cm. CMR điểm D di động trên đươngf tròn cố định
Làm giups mk nha mk đag cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 1 2019
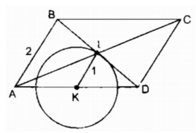
Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = 1/2 AB = 1/2.2 = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K; 1 cm)
TP
28 tháng 1 2018
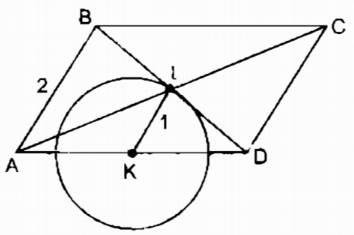
Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = \(\dfrac{1}{2}AB=\dfrac{1}{2}.2\) = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K ; 1 cm)
DD
2
VH
22 tháng 6 2019
Thật ra thì phải lấy kiến thức lớp 11 về phép tịnh tiến để giải bài này