Một viên đá có khối lượng 0,2 kg được buộc vào sợi dây dài 30 cm và quay thành hình tròn trong mặt phẳng ngang. Biết rằng, sợi dây đứt khi lực căng vượt quá 0,8 N. Tính tốc độ tối đa mà viên đá được quay mà sợi dây vẫn chưa bị đứt.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm: Fht = P + T → T = Fht - P
⟹ T = mω2r – mg = 0,4.82.0,5 – 0,4.9,8 = 8,88 N.

Đáp án A
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm.


Chọn A.
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
F h t = P + T → T = F h t - P
⟹ T = m ω 2 r – mg
= 0,4. 8 2 .0,5 – 0,4.9,8 = 8,88 N.

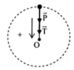
+ Các lực tác dụng lên vật khi đó gồm trọng lực P → và lực căng dây T →
+ Vì vật chuyển động tròn đều nên
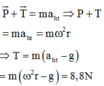
=> Chọn A.

Chọn đáp án A
Khi hòn đá ở đỉnh của đường tròn thì trọng lực và lực căng dây đóng vai trò là lực hướng tâm:
Fht = P + T
→ T = Fht - P
T = mω2r – mg
= 0,4.05 – 0,4.9,8 = 8,88 N.

Khi dây đứt, hòn đá chuyển động như một vật bị ném ngang với vận tốc
v = ω r = ω lsin α = 3,14.1,00. 0,1167 = 0,366 m/s
Thời gian từ khi hòn đá bị văng ra đến khi chạm đất
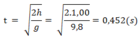
s = vt = 0,366.0,452 = 0,165 m = 16,5 cm.

Đáp án B
Tốc độ dài của viên bi lúc dây đứt là
![]()
Chọn trục Ox thẳng đứng hướng xuống gốc O tại vị trí viên bi khi bị đứt dây, gốc thời gian là lúc dây bị đứt. Phương trình chuyển động của viên bi là
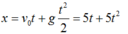
Khi viên bi chạm đất thì:
![]()
![]()
![]()
![]()
Chú ý: Sau khi xác định được tốc độ của viên bi tại thời điểm đứt dây, bài toán trở thành bài toán ném vật thẳng đứng hướng xuống.

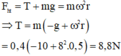
Tham khảo:
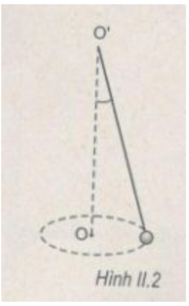
Chọn hệ quy chiếu như hình vẽ
Theo định luật II Newton ta có: \(\overrightarrow P + \overrightarrow T = \overrightarrow {{F_{ht}}} \) (1)
Từ hình vẽ ta có: R = l.sinα
Chiếu (1) lên trục Ox có:
\(\begin{array}{l}T.\sin \alpha = {F_{ht}}\\ \Leftrightarrow T.\sin \alpha = m.\frac{{{v^2}}}{R} \Leftrightarrow {v^2} = \frac{{T.\sin \alpha .R}}{m}\\ \Leftrightarrow {v^2} = \frac{{T.l.{{\sin }^2}\alpha }}{m} \Rightarrow {v_{\max }} \Leftrightarrow {T_{\max }},\sin \alpha = 1\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.l}}{m}} = \sqrt {\frac{{0,8.0,3}}{{0,2}}} \approx 1,1(m/s)\end{array}\)