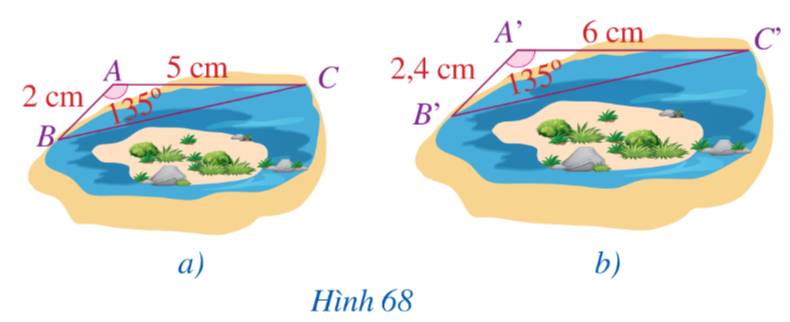
Quan sát hình 68 và so sánh:
a) Các tỉ số \(\frac{{A'B'}}{{AB}}\) và \(\frac{{A'C'}}{{AC}}\)
b) Các góc \(\widehat A\) và \(\widehat {A'}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.
CM
8 tháng 2 2018
a)
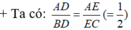
Nên theo định lí ta- let đảo ta có: DE // BC.
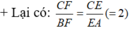
Nên theo định lí ta- let đảo ta có: EF // AB.
b) Tứ giác BDEF là hình bình hành vì có các cặp cạnh đối song song với nhau
c) Tứ giác BDEF là hình bình hành ⇒ DE = BF = 7
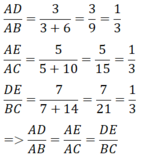
Ba cạnh của ΔADE tương ứng tỉ lệ với ba cạnh của ΔABC
7 tháng 4 2017
- Hình dạng của tháp: cả hai tháp đều có đáy rộng, đỉnh nhọn nhưng chân của đáy ở nhóm 0 – 4 tuổi của năm 1999 đã thu hẹp hơn so với năm 1989.
- Cơ cấu dân số theo độ tuổi:
+ Năm 1989: nhóm tuổi 0 – 14 : 39%, nhóm tuổi : 15 -59: 53,8%, nhóm tuổi trên 60 : 7,2 % . Năm 1999: nhóm tuổi 0 – 14 : 33,5 %, nhóm tuổi : 15 -59: 58,4 %, nhóm tuổi trên 60 : 8,1 %
+ Tuổi dưới và trong độ tuổi lao động đều cao nhưng độ tuổi dưới lao động năm 1999 nhỏ hơn năm 1989. Độ tuổi lao động và ngoài lao động năm 1999 cao hơn năm 1989.
- Tỉ lệ dân số phụ thuộc còn cao (năm 1989 : 85,8%, năm 1999: 71,2%)
(tỉ lệ phụ thuộc : tỉ số giữa người chưa đến độ tuổi lao động, số người quá tuổi lao động với những người đang trong độ tuổi lao động của dân cư một vùng, một nước).
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)
Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).
b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)
Vậy \(\widehat {AMN} = 65^\circ \).
13 tháng 9 2023
a: AM/AB=AN/AC=MN/BC=4/12=1/3
b: góc AMN=góc ABC=65 độ
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
Hai điểm biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) cách gốc 0 một khoảng bằng nhau.
9 tháng 9 2016
- Hình 1.3, các nước phát triển : tỉ lệ sinh tăng vào đầu thế kỉ XIX, nhưng đến cuối thế kỉ XIX, đầu thế kỉ XX giảm rất nhanh ; tỉ lệ tử giảm rất nhanh đến giữa thế kỉ XX, sau đó ổn định lại và có tăng trong giai đoạn 1980-2000. Gia tăng dân số tự nhiên tăng nhanh trong giai đoạn 1800-1850, nhưng giảm nhanh vào giai đoạn 1850-2000.
- Hình 1.4, các nước đang phát triển : tỉ lệ sinh cao và giữ ổn định trong một thời gian dài từ 1800 đến 1950, sau đó giảm mạnh vào giai đoạn 1950-2000 nhưng vẫn ờ mức cao ; tỉ lệ tử giảm rất nhanh ; gia tăng dân số tự nhiên tăng nhanh và dẫn tới bùng nổ dân số từ những năm 1950 đến 2000
21 tháng 9 2017
Trả lời:
- Hình 1.3, các nước phát triển : tỉ lệ sinh tăng vào đầu thế kỉ XIX, nhưng đến cuối thế kỉ XIX, đầu thế kỉ XX giảm rất nhanh ; tỉ lệ tử giảm rất nhanh đến giữa thế kỉ XX, sau đó ổn định lại và có tăng trong giai đoạn 1980-2000. Gia tăng dân số tự nhiên tăng nhanh trong giai đoạn 1800-1850, nhưng giảm nhanh vào giai đoạn 1850-2000.
- Hình 1.4, các nước đang phát triển : tỉ lệ sinh cao và giữ ổn định trong một thời gian dài từ 1800 đến 1950, sau đó giảm mạnh vào giai đoạn 1950-2000 nhưng vẫn ờ mức cao ; tỉ lệ tử giảm rất nhanh ; gia tăng dân số tự nhiên tăng nhanh và dẫn tới bùng nổ dân số từ những năm 1950 -2000
còn câu kia thì .....
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
27 tháng 5 2023
Đ/điểm | Màu sắc | Kích thước | Hình dạng |
Hoa đào | Hồng | Bé | Hình tròn Nhiều cánh Các lớp cánh hoa xếp chồng |
Hoa mai | Vàng | Bé | Hình tròn Nhiều cánh Các lớp cánh hoa xếp chồng |
Hoa sen | Hồng | Lớn | Hình tròn Cánh to, vòm, đầu dánh vót nhọn |
Hoa phượng vĩ | Đỏ | Bé | Cánh dài, đầu cánh có viền nhăn. |
Hoa hồng | Đỏ | Vừa | Hình tròn Nhiều cánh Các lớp cánh hoa xếp chồng |
Hoa huệ | Trắng | Lớn | Hình dài, xòe ra ở phần cánh hoa Đầu nhụy dài, rỗng, 5 cánh hoa |
=> Mỗi loài hoa có màu sắc, kích thước, hình dạng khác nhau.
HQ
Hà Quang Minh
Giáo viên
26 tháng 8 2023
Tỉ số truyền của hộp số nhỏ hơn khi bánh răng số 7 bên trái được nối vào với trục thứ cấp.
5 tháng 9 2018
- Quan sát hình 67 (rừng mưa nhiệt đới), ta thấy: rừng rậm với nhiều loài cây chen chúc, mọc thành nhiều tầng. Nguyên nhân là do có khí hậu nóng, ẩm quanh năm.
- Quan sát hình 67 (hoang mạc nhiệt đới), ta thấy: thực vật cằn cỗi, thưa thớt, lác đác chỉ có một vài cây xương rồng và những bụi cỏ gai. Nguyên nhân là do tính chất khí hậu vô cùng khô hạn.
a) Ta có:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{{2,4}} = \frac{5}{6}\\\frac{{A'C'}}{{AC}} = \frac{5}{6}\end{array}\)
Vậy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
b) Ta có: \(\widehat A = \widehat {A'} = 135^\circ \)