cho góc xoy = 80độ, góc yoz kề bù vs góc xoy. gọi ot là tia phân giác của góc xoy tìm các số đo xot và toz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 4 2016
Ta có : xOy+yOz=180 độ(2 góc kề bù)
Vì xOy=5/4 yOz
=> 5/4yOz+yOz=180 độ
=> 9/4 yOz=180
=> yOz=180:9/4
=> yOz=80 độ
Mà xOy+yOz=180 độ
Hay xOy+80 độ =180 độ
=> xOy=180độ - 80 độ=100 độ
7 tháng 3 2021
Ta có: xOy+yOz =180 đo (2 góc kề bù)
=> yOz=180-xOy=180-80=100
Vì Ot là tia phân giác góc yOz nên yOt=tOz=1/2 yOz=50
Trên cùng nửa mặt phẳng có bờ chứa tia Ox (câu này có thể thiếu hay sai gì đó, vì lâu rồi chưa đụng lại toán lớp 6) nên xOy<xOy (80<180) nên Oy nằm giữa Ox và Oy.
Mà Ot nằm giữa Oz và Oy (vì Ot là tia phân giác góc yOz) nên Oy nằm giữa Ox và Ot.
=>xOt=xOy+yOt=80+50 =130
Vậy yOt=50, xOt=130
CM
14 tháng 8 2018
Ta có y O z ^ = 130 ° . Để Ot là tia phân giác của góc yOz thì z O t ^ = y O z ^ 2 = 65 ° . Khi đó, theo tính chất cộng góc, ta suy ra
x O t ^ = 180 ° - 65 ° = 115 °
CM
23 tháng 7 2018
Ta có y O z ^ = 130°. Để Ot là tia phân giác của góc yOz thì z O t ^ = y O z ^ 2 = 65 ° . Khi đó, theo tính chất cộng góc, ta suy ra
x O t ^ = 180°- 65°= 115°
CM
6 tháng 7 2019
Đáp án là B
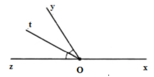
Vì ∠xOy và ∠yOz là hai góc kề bù nên ∠xOy + ∠yOz = 180 0 mà ∠xOy = 120 0 nên ∠yOz = 180 0 - 120 0 = 60 0
Lại có tia Ot là tia phân giác của ∠yOz nên
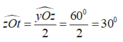
Lại có ∠zOt; ∠tOx là hai góc kề bù nên
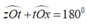
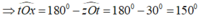
Vậy ∠tOx = 150 0
14 tháng 5 2021
a)Vì xOy và yOz là 2 góc kề bù nên:
xOy+yOz=180*
40*+ yOz=180*
yOz=180*-40*=140*
b)Vì Ot là tia phân giác của góc yOz nên:
yOt=\(\dfrac{zOt}{2}\)=\(\dfrac{140}{2}\)=70*
Vì tOy và yOx là 2 góc kề nhau:
\(\rightarrow\)Tia Oy nằm giữa 2 tia Ot và Ox
\(\rightarrow\) tOy+yOx=xOt
70*+40* =xOt
\(\Rightarrow\) 70*+40* =110*
14 tháng 5 2021
A. xoy + yoz =180o
40o +yoz = 180o
yoz = 180-40
yoz = 140o
Vậy.....
b. Tia ot là tia phân giác của yoz nên
toy = \(\dfrac{yoz}{2}\) = \(\dfrac{140}{2}\) = 120o
vì tia ot nằm giữa oy và oz mà tia oy lại nằm giữa tia õ và oz.
Suy ra tia oy nằm giữa tia õ và ot
Nên xoy + yot = xot
xot = 140 + 120
xot = 160o
Vậy ot = 160o
Ta có :
\(\widehat{xOy}+\widehat{yOz}=180^o\) (2 góc kề bù)
\(\Rightarrow\widehat{yOz}=180^o-\widehat{xOy}\)
\(\Rightarrow\widehat{yOz}=180^o-80^o\)
\(\Rightarrow\widehat{yOz}=100^o\)
Ta lại có :
\(\widehat{tOz}=\widehat{tOy}+\widehat{yOz}\)
mà \(\widehat{tOy}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.80^o=40^o\) (Ot là phân giác góc xOy)
\(\Rightarrow\widehat{tOz}=40^o+100^o\)
\(\Rightarrow\widehat{tOz}=140^o\)
\(\widehat{xOt}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.80^o=40^o\) (Ot là phân giác góc xOy)