Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE = AC.AM và An lần lượt là các đường trung tuyến của Tam giác bác và đe a) bm=dn b) chứng minh góc bam=dan c) chứng minh góc mad kề bù vs dan suy ra m,a,n thằng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
25 tháng 8 2023
Đúng(0)
Những câu hỏi liên quan
14 tháng 8 2020
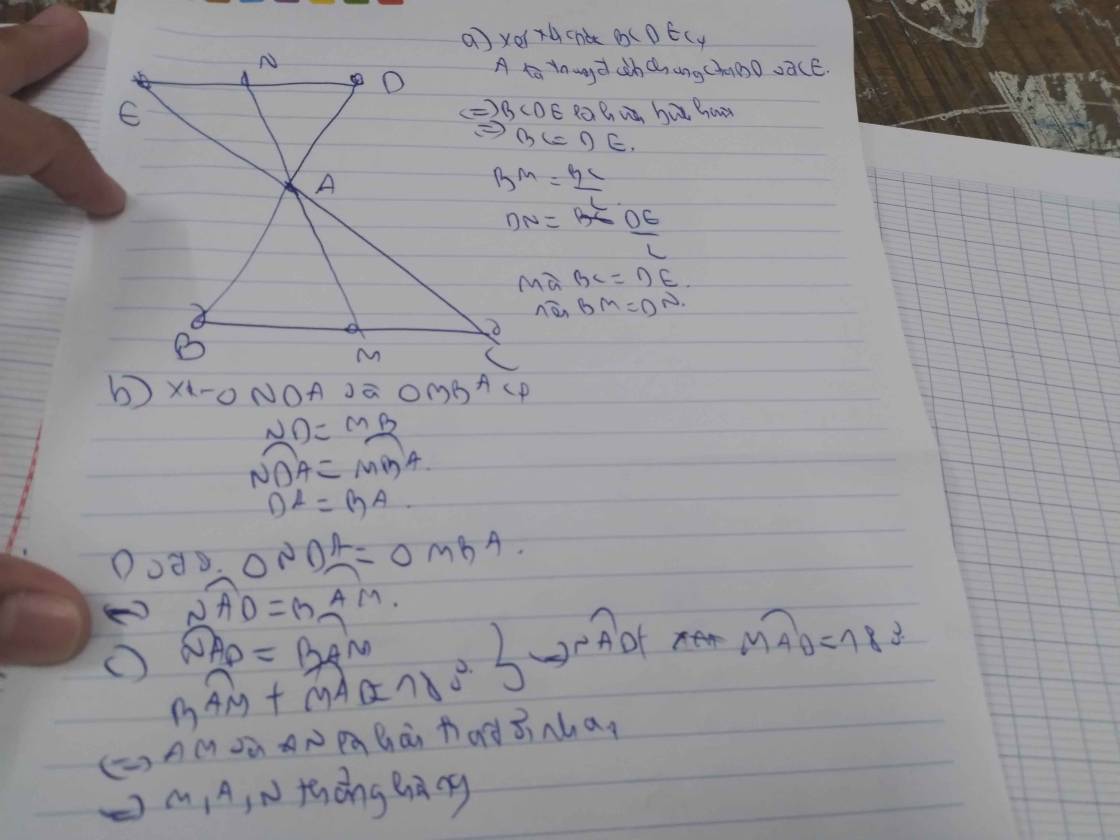
a)
Có: \(AD=AB;AE=AC\)
=> \(\frac{AD}{AB}=1;\frac{AE}{AC}=1\)
=> \(\frac{AD}{AB}=\frac{AE}{AC}=1\)
Áp dụng định lí Talet đảo ta được:
=> DE // BC.
=> \(NDA=ABM\) (2 góc ở vị trí so le trong)
Xét tam giác ABM và tam giác ADN có:
\(\hept{\begin{cases}AB=AD\left(gt\right)\\ABM=ADN\left(cmt\right)\\BM=DN\left(gt\right)\end{cases}}\)
=> Tam giác ABM = Tam giác ADN (cgc)
=> TA CÓ ĐPCM.
b) Do Tam giác ABM = Tam giác ADN (cmt)
=> \(BAM=DAN\)
Áp dụng định lí Talet khi BC // DE ta được:
=> \(\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}\)
Mà: \(\frac{AD}{AB}=\frac{AE}{AC}=1\left(cmt\right)\)
=> \(\frac{DE}{BC}=1\Rightarrow DE=BC\)
Mà: \(BM=DN\left(gt\right)\Rightarrow NE=MC\)
Khi đó, CMTT: Tam giác AMC = Tam giác ANE (cgc)
=> \(MAC=NAE\)
Ta có: \(BAC+ABC+ACB=180\) (ĐỊNH LÍ TỔNG 3 GÓC TRONG TAM GIÁC)
=> \(BAM+MAC+ABC+ACB=180\) (1)
Mà: E, A, C là 3 điểm thẳng hàng
=> góc EAB là góc ngoài của tam giác ABC
=> \(EAB=ABC+ACB\) (2)
Và: \(MAC=EAN\left(cmt\right)\) (3)
TỪ (1); (2) VÀ (3) TA ĐƯỢC:
=> \(BAM+NAE+BAE=180\)
=> \(NAM=180\)
=> 3 điểm M, N, A thẳng hàng.
VẬY TA CÓ ĐPCM.
TT
14 tháng 8 2020
a) xét \(\Delta ADE\)VÀ \(\Delta ABC\)CÓ
\(AD=AB\left(gt\right);\widehat{DAE}=\widehat{BAC}\left(Đ^2\right);AE=AC\left(gt\right)\)
=> \(\Delta ADE\)=\(\Delta ABC\)(c-g-c)
=> \(\widehat{ADE}=\widehat{ABC}\)( hai góc tương ứng ) hay \(\widehat{ADN}=\widehat{ABM}\)
xét \(\Delta ABM\)VÀ \(\Delta ADN\)CÓ
\(BM=DM\left(gt\right);\widehat{ADN}=\widehat{ABM}\left(cmt\right);AB=AD\left(gt\right)\)
=>\(\Delta ABM\)=\(\Delta ADN\)(c-g-c)
b tối tớ suy nghỉ
10 tháng 12 2021
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
24 tháng 9 2022
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: AM=ED/2
AN=BC/2
mà ED=BC
nên AM=AN
18 tháng 12 2020
a)
Sửa đề: ΔABM=ΔADN
Xét ΔAED và ΔACB có
AE=AC(gt)
\(\widehat{EAD}=\widehat{CAB}\)(hai góc đối đỉnh)
AD=AB(gt)
Do đó: ΔAED=ΔACB(c-g-c)
⇒\(\widehat{ADE}=\widehat{ABC}\)(hai góc tương ứng)
hay \(\widehat{ADN}=\widehat{ABM}\)
Xét ΔADN và ΔABM có
DN=BM(gt)
\(\widehat{ADN}=\widehat{ABM}\)(cmt)
AD=AB(gt)
Do đó: ΔADN=ΔABM(c-g-c)
b) Ta có: ΔADN=ΔABM(cmt)
nên \(\widehat{DAN}=\widehat{BAM}\)(hai góc tương ứng)
mà \(\widehat{BAM}+\widehat{DAM}=180^0\)(hai góc kề bù)
nên \(\widehat{DAN}+\widehat{DAM}=180^0\)
\(\Leftrightarrow\widehat{NAM}=180^0\)
hay M,A,N thẳng hàng(đpcm)
8 tháng 4 2022
1: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó; BCDE là hình bình hành
Suy ra: BC//DE
2: AH\(\perp\)BC
mà BC//DE
nên \(AH\perp\)DE
mà AK\(\perp\)DE
và AH,AK có điểm chung là A
nên H,A,K thẳng hàng
LD
9 tháng 8 2017
Mình thấy đề sai rồi vì giả thiết đã cho N thuộc ED nên E, N, D thẳng hàng.
Mình sửa lại đề là chứng minh M, A, N thẳng hàng.
Ta dễ dàng chứng minh tam giác ABC = tam giác ADE ( c - g - c)
=> BC = DE ( 2 cạnh tương ứng)
Ta chứng minh tam giác ABM = tam giác ADN có:
AB = AD (gt)
BM = DN (gt)
góc ABM = góc ADN ( tam giác ABC = tam giác ADE)
=> góc BAM = góc DAN ( 2 góc tương ứng)
Mà 2 góc này nằm ở vị trí đối đỉnh nên M, A, N thẳng hàng.
HT
9 tháng 8 2017
cái đó đã chứng minh rồi ạ bây h phải chứng minh E,N,D thẳng hàng p ạ