Tìm tham số m để:
a) d: y = 2mx + 5 và d': y = 4x +m cắt nhau tại điểm có hoành độ bằng 1.
b) d: y = (3m - 2)x + 4 cắt trục hoành tại điểm có hoành độ bằng 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m^2-2=2\\m-1\ne-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2=4\\m\ne-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\in\left\{2;-2\right\}\\m\ne-2\end{matrix}\right.\)
=>m=2
b: Để (d) trùng với (d2) thì
\(\left\{{}\begin{matrix}m^2-2=-1\\m-1=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m^2=1\\m=-1\end{matrix}\right.\)
=>m=-1
c:
Để (d) cắt (d3) thì \(m^2-2\ne3\)
=>\(m^2\ne5\)
=>\(m\ne\pm\sqrt{5}\)
Thay x=-1 vào y=3x-2, ta được:
\(y=3\left(-1\right)-2=-5\)
Thay x=-1 và y=-5 vào (d), ta được:
\(-\left(m^2-2\right)+m-1=-5\)
=>\(-m^2+2+m-1+5=0\)
=>\(-m^2+m+6=0\)
=>\(m^2-m-6=0\)
=>(m-3)(m+2)=0
=>\(\left[{}\begin{matrix}m-3=0\\m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\left(nhận\right)\\m=-2\left(nhận\right)\end{matrix}\right.\)
d: Để (d) vuông góc với (d4) thì \(\dfrac{4}{5}\left(m^2-2\right)=-1\)
=>\(m^2-2=-1:\dfrac{4}{5}=-\dfrac{5}{4}\)
=>\(m^2=\dfrac{3}{4}\)
=>\(m=\pm\dfrac{\sqrt{3}}{2}\)

a, Khi m = 1 ta có d : y = 2x – 1 và (P): y = –x2
Phương trình hoành độ giao điểm của d và (P) là:
Với x = − 1 + 2 ⇒ y = − 3 + 2 2
Với x = − 1 − 2 ⇒ y = − 3 − 2 2
Vậy các giao điểm là − 1 + 2 ; − 3 + 2 2 ; − 1 − 2 ; − 3 − 2 2

a: Để (d)//(d') thì \(\left\{{}\begin{matrix}k-2=2\\-k\ne4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}k=4\\k\ne-4\end{matrix}\right.\)
=>k=4
b: Để (d) vuông góc (d') thì \(2\left(k-2\right)=-1\)
=>2k-4=-1
=>2k=3
=>\(k=\dfrac{3}{2}\)
c: Để (d) cắt (d') thì \(k-2\ne2\)
=>\(k\ne4\)

a.
Để hai đường thẳng song song:
\(\Rightarrow\left\{{}\begin{matrix}2m=-\dfrac{1}{3}\\m-1\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{1}{6}\\m\ne2\end{matrix}\right.\) \(\Leftrightarrow m=-\dfrac{1}{6}\)
b.
\(-2x-y=5\Leftrightarrow y=-2x-5\)
Để hai đường thẳng trùng nhau:
\(\Leftrightarrow\left\{{}\begin{matrix}2m=-2\\m-1=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m=-4\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
Vậy ko tồn tại m để 2 đường thẳng trùng nhau

a, Hoành độ giao điểm của d và P là:
x2 = 2mx -m +1 <=> x2 -2mx +m-1
đenta = 4m2-4.(m-1) = 4m2-4m+4 = (2m)2-2.2m +1 +3=(2m-1)2+3
=> đenta >= 3
Vậy không có giá trị m để P tiếp xúc với d
b,Áp dụng định lí Vi-ét:
\(\left\{{}\begin{matrix}x1+x2=2m\\x1.x2=m-1\end{matrix}\right.\)
Ta có: x12.x2 + mx2=x2
<=> x12.x2+mx2-x2=0 <=> x12.x2 + x2(m-1)=0
<=> x12.x2+x2(x1.x2)=0 <=>x12.x2+x22.x1=0
<=>x1.x2.(x1+x2)=0 <=> (m-1).2m=0
<=> \(\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Vậy m \(\in\) \(\left\{1;0\right\}\)

Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)

a) Để (d) đi qua M(2;5) thì Thay x=2 và y=5 vào (d), ta được:
\(2m\cdot2-2m+3=5\)
\(\Leftrightarrow4m-2m=5-3\)
\(\Leftrightarrow2m=2\)
\(\Leftrightarrow m=1\)
Vậy: Để (d) đi qua M(2;5) thì m=1
b) Phương trình hoành độ của (d) và (P) là:
\(x^2=2mx-2m+3\)
\(\Leftrightarrow x^2-2mx+2m-3=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(2m-3\right)=4m^2-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=4m^2-8m+12=\left(2m\right)^2-2\cdot2m\cdot2+4+8\)
\(\Leftrightarrow\Delta=\left(2m-2\right)^2+8>0\forall m\)
Suy ra: (d) và (P) luôn cắt nhau tại hai điểm phân biệt với mọi m

Đáp án: D.
Tập xác định: D = R \ {m}
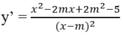
Hàm số có cực trị khi và chỉ khi y' đổi dấu trên D
⇔ x 2 - 2mx + 2 m 2 - 5 = 0 có hai nghiệm phân biệt
⇔ ∆ ' = - m 2 + 5 > 0 ⇔ - 5 < m < 5
a: Thay x=1 vào y=4x+m, ta được:
y=4*1+m=m+4
Thay x=1 và y=m+4 vào y=2mx+5, ta được:
2m+5=m+4
=>m=-1
b: Thay x=3 và y=0 vào (d), ta được:
3(3m-2)+4=0
=>9m-6+4=0
=>9m-2=0
=>m=2/9