cho tam giác abc vuông tại C, biết cos C =5/13, tính TSLG góc B Giúp vs ;-;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2021
\(a,BC=\sqrt{AB^2+AC^2}=15\left(cm\right)\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot CH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\\CH=\dfrac{AC^2}{BC}=9,6\left(cm\right)\\AH=\sqrt{5,4\cdot9,6}=51,84\left(cm\right)\end{matrix}\right.\)
\(b,\sin B=\cos C=\dfrac{AC}{BC}=\dfrac{4}{5}\\ \cos B=\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\\ \tan B=\cot C=\dfrac{AC}{AB}=\dfrac{4}{3}\\ \cot B=\tan C=\dfrac{AB}{AC}=\dfrac{3}{4}\)
12 tháng 8 2016
a) ta xét tam giác ABC có :
\(AB^2+BC^2=5^2+12^2=AC^2=13^2\)
yheo định lí đảo pitgo
=> tam giavs ABC vuông tại B
b) ta có sin A=\(\frac{BC}{AC}=\frac{12}{13}\)
cosA=\(\frac{AB}{AC}=\frac{5}{12}\)
tan A=\(\frac{BC}{AB}=\frac{12}{5}\)
cotA =\(\frac{AB}{BC}=\frac{5}{12}\)
sin C=cosA=\(\frac{5}{12}\)
cosC=sinA=\(\frac{12}{13}\)
tanC =cot A=\(\frac{5}{12}\)
cotC=tanC=\(\frac{12}{5}\)
NL
1
21 tháng 8 2016
tam giác ABC vuông tại C
=> \(\sin B=\cos A=\frac{5}{15}\)
=> \(\sin^2B+\cos^2B=1\) => \(\cos B=\sqrt{1-\sin^2B}\)= \(\sqrt{1-\frac{5}{13}}=\sqrt{\frac{8}{13}}\)
=> \(\tan B=\frac{\sin B}{\cos B}=\frac{\frac{5}{13}}{\sqrt{\frac{8}{13}}}=\frac{\sqrt{26}}{12}\) \(\cot B=\frac{1}{\tan B}=\frac{12}{\sqrt{26}}\)
ok mk nhé!! 34435345354457688799234324134564556565765575776876456
3 tháng 10 2021
Ta có: ΔABC vuông tại A
mà \(AC=\dfrac{1}{2}BC\)
nên \(\widehat{B}=30^0\)
\(\sin\widehat{B}=\dfrac{1}{2}\)
\(\cos\widehat{B}=\dfrac{\sqrt{3}}{2}\)
\(\tan\widehat{B}=\dfrac{\sqrt{3}}{3}\)
\(\cot\widehat{B}=\sqrt{3}\)
HL
1
5 tháng 10 2021
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=8(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\dfrac{3}{5}\)
\(\tan\widehat{B}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{3}{4}\)
6 tháng 10 2021
a: Xét ΔMNE vuông tại M có
\(MN^2+ME^2=NE^2\)
hay ME=4(cm)
DT
1
10 tháng 9 2019
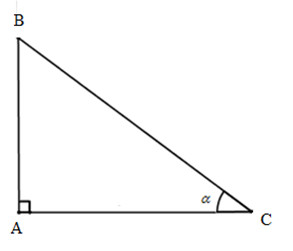
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Ta có:
Sin2C+cos2C=1Sin2C+cos2C=1
⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;⇒cosC=0,6;
tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;
cotgC=cosCsinC=0,60,8=34
Xem lại đề nhé bạn đề sai rồi