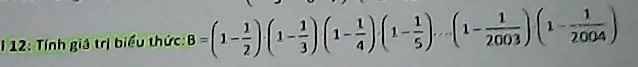
Giải hộ tớ nhé đang gấp :00
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VL
12 tháng 11 2023
Gọi chiều dài của miếng đất là x (m), chiều rộng của miếng đất là y (m) (x>y>0)(�>�>0)
Do miếng đất có chu vi 56m nên ta có phương trình
2(x+y)=56⇔x+y=28(1)2(�+�)=56⇔�+�=28(1)
Nếu tăng chiều rộng lên 4m thì chiều rộng mới là y+4(m)�+4(�)
Giảm chiều dài đi 4m thì chiều dài mới là x−4(m)�−4(�)
Diện tích ban đầu là xy(m2)��(�2)
Diện tích lúc sau là (x−4)(y+4)(m2)(�−4)(�+4)(�2)
Vì diện tích tăng thêm 8 m2 nên ta có phương trình
(x−4)(y+4)−xy=8⇔xy+4x−4y−16−xy=8⇔4x−4y=24⇔x−y=6(2)(�−4)(�+4)−��=8⇔��+4�−4�−16−��=8⇔4�−4�=24⇔�−�=6(2)
Từ (1) và (2) ta có hệ phương trình
{x+y=28x−y=6⇔{2x=34x+y=28⇔{x=17y=11(tm){�+�=28�−�=6⇔{2�=34�+�=28⇔{�=17�=11(��)
Vậy chiều dài của miếng đất là 17m, chiều rộng của miếng đất là 11m.
tik nha
21 tháng 3 2022
TL:
Chiều rộng mảnh đất là:
90 : 5 x 3 = 54 (m)
Chu vi mảnh đất là:
(90 + 54) x 2 = 288 (m)
Diện tích mảnh đất là:
90 x 54 = 4860 (m2)
Đáp số: Chu vi: 288 m ; Diện tích: 4860 m2.
HT
21 tháng 3 2022
Chiều rộng mảnh đất là:
90×35=54(m)
Chu vi mảnh đất là:
(90+54)×2=288(m)
Diện tích mảnh đất là:
90×54=4860(m)
MS
3
LN
1
NT
19 tháng 11 2017
3
Có\(S_{GCBH}=a^2\)
\(S_{CDEA}=b^2\)
\(S_{BAKI}=c^{^2}\)
Áp dụng định lý Py ta go vào tam giác ABC
\(BC^{^2}=AB^2+AC^2\) hay \(a^2=b^2+c^2\)
Vậy Đpcm
4 tháng 11 2017
4.Viết PTHH cho mối chuyển đổi sau :
a) (1) CaO + CO2 \(\rightarrow CaCO_3\)
(2) CaCO3 \(\rightarrow\) CaO + CO2
(3) CaO + H2O \(\rightarrow\) Ca(OH)2
(4) CaO + HCl \(\rightarrow\) CaCl2 + H2O
b) (1) S + O2 \(\rightarrow\) SO2
(2) SO2 + Na2O \(\rightarrow\) Na2SO3
(3) Na2SO3 \(\rightarrow\) SO2 + Na2O
(4) SO2 + H2O \(\rightarrow\) H2SO3
chúc bạn học tốt nha . #ah_kiêu 
12:
\(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{5}\right)...\left(1-\dfrac{1}{2004}\right)\)
\(B=\left(\dfrac{2}{2}-\dfrac{1}{2}\right)\left(\dfrac{3}{3}-\dfrac{1}{3}\right)\left(\dfrac{4}{4}-\dfrac{1}{4}\right)...\left(\dfrac{2004}{2004}-\dfrac{1}{2004}\right)\)
\(B=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot\dfrac{4}{5}...\cdot\dfrac{2003}{2004}\)
\(B=\dfrac{1\cdot2\cdot3\cdot...\cdot2002\cdot2003}{2\cdot3\cdot4\cdot...\cdot2003\cdot2004}\)
\(B=\dfrac{1}{2004}\)
`12) B=(1-1/2)(1-1/3)(1-1/4)(1-1/5)....(1-1/2003)(1-1/2004)`
`B=1/2 . 2/3 . 3/4 . 4/5 .... 2002/2003 . 2003/2004`
`B= [1.2.3.4......2002.2003]/[2.3.4.5.....2003.2004]`
`B=1/2004`
`7)`
`a)[254xx399-145]/[254+399xx253]`
`=[(253+1)xx399-145]/[254+399xx253]`
`=[253xx399+399-145]/[254+399xx253]`
`=[254+253xx399]/[254+253xx399]=1`
`b)[5932+6001xx5931]/[5932xx6001-69]`
`=[5932+6001xx5931]/[(5931+1)xx6001-69]`
`=[5932+6001xx5931]/[5931xx6001+6001-69]`
`=[5932+6001xx5931]/[5932+6001xx5931]=1`