Xét tính bị chặn của un
•un= 5/(n²+1) + (n+2)/(n+1) + cos(n)
•un=1/(n²+1) + sin(n)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


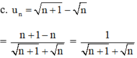
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
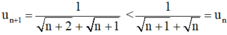
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.

\(u_n=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{n\left(n+1\right)}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(=1-\dfrac{1}{n+1}< 1\)
=>Hàm số bị chặn trên tại \(u_n=1\)
\(n+1>=1\)
=>\(\dfrac{1}{n+1}< =1\)
=>\(-\dfrac{1}{n+1}>=-1\)
=>\(1-\dfrac{1}{n+1}>=-1+1=0\)
=>Hàm số bị chặn dưới tại 0
\(u_n=1-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
\(\dfrac{u_n}{u_{n+1}}=\dfrac{n}{n+1}:\dfrac{n+1}{n+2}=\dfrac{n^2+2n}{n^2+2n+1}< 1\)
=>(un) là dãy số tăng

\(u_n=\dfrac{1}{n+1}\Rightarrow u_{n+1}=\dfrac{1}{n+2}\)
\(\Rightarrow u_n-u_{n+1}=\dfrac{1}{n+1}-\dfrac{1}{n+2}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}>0\)
\(\Rightarrow u_{n+1}< u_n\Rightarrow\) dãy giảm
Do \(\dfrac{1}{n+1}>0\Rightarrow\) dãy bị chặn dưới bởi 0
\(u_n-1=\dfrac{1}{n+1}-1=-\dfrac{n}{n+1}< 0\Rightarrow u_n< 1\)
\(\Rightarrow\) Dãy bị chặn trên bởi 1
\(\Rightarrow\) Dãy bị chặn

Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 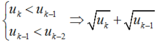
![]()
Vậy dãy (un) là dãy tăng và bị chặn.

Chọn B.
Trước hết bằng quy nạp ta chứng minh: (un) 1 < un ≤ 2, ∀ n
Điều này đúng với n = 2, giả sử 1 < un < 2 ta có: ![]() nên ta có đpcm.
nên ta có đpcm.
Mà ![]() .
.
Vậy dãy (un) là dãy giảm và bị chặn.

Do \(n\in N\Rightarrow n+1>0\Rightarrow u_n=\dfrac{1}{n+1}>0\Rightarrow u_n\) bị chặn dưới bởi 0
Do \(n\in N\Rightarrow n\ge0\Rightarrow n+1\ge1\Rightarrow\dfrac{1}{n+1}\le1\)
\(\Rightarrow u_n\) bị chặn trên bởi 1
\(\Rightarrow\) Dãy số đã cho là dãy bị chặn