Cho hình chóp tam giác \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,SA \bot \left( {ABC} \right)\). Tính \(d\left( {SA,BC} \right)\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(\left(SBC\right)\cap\left(ABC\right)=BC\)
Lấy H là TĐ của BC \(\Rightarrow AH\perp BC\)
SA \(\perp\left(ABC\right)\Rightarrow SA\perp AB;AC\)
\(\Delta SAB;\Delta SAC\perp\) tại A có : \(SB=\sqrt{SA^2+AB^2}=\sqrt{SA^2+AC^2}=SC\)
\(\Rightarrow\Delta SBC\) cân tại S . Suy ra : \(SH\perp BC\)
Suy ra : \(\left(\left(SBC\right);\left(ABC\right)\right)=\left(HA;HS\right)=\widehat{SHA}\)
Tính được : AH = \(\dfrac{a\sqrt{3}}{2}\)
\(\Delta SAH\) vuông tại A có : \(tan\widehat{SHA}=\dfrac{SA}{HA}=\dfrac{a\sqrt{3}}{2}:\dfrac{a\sqrt{3}}{2}=1\Rightarrow\widehat{SHA}=45^o\)
Vậy ...

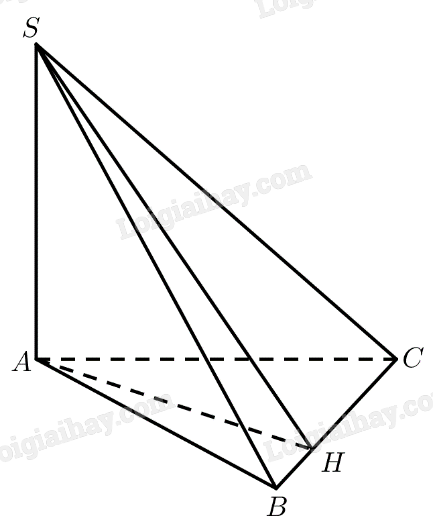
Kẻ \(AH \bot BC\left( {H \in BC} \right)\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)
\( \Rightarrow \widehat {SHA} = \alpha \)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)

\(BP=\dfrac{1}{3}AB\Rightarrow BP=\dfrac{1}{2}AP\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}d\left(A;\left(SPC\right)\right)\)
Trong tam giác APC, kẻ \(AH\perp CP\Rightarrow CP\left(SAH\right)\)
Trong tam giác vuông SAH, kẻ \(AK\perp SH\Rightarrow AK\perp\left(SPC\right)\Rightarrow AK=d\left(A;\left(SPC\right)\right)\)
\(AP=\dfrac{2}{3}AB=\dfrac{2a}{3}\Rightarrow CP=\sqrt{AP^2+AC^2-2AP.AC.cos60^0}=\dfrac{a\sqrt{7}}{3}\)
Áp dụng định lý hàm sin:
\(\dfrac{AP}{sin\widehat{ACP}}=\dfrac{CP}{sinA}\Rightarrow sin\widehat{ACP}=\dfrac{AP.sin60^0}{CP}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow AH=AC.sin\widehat{ACP}=\dfrac{a\sqrt{21}}{7}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{2a\sqrt{93}}{31}\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}AK=\dfrac{a\sqrt{93}}{31}\)
Bạn kiểm tra lại phần tính toán

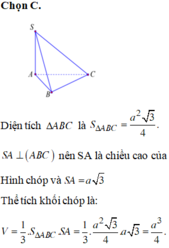
Chọn C.

Diện tích ∆ ABC là S A B C = a 2 3 4
SA ⊥ (ABC) nên SA là chiều cao của hình chóp và SA= a 3
Thể tích khối chóp là
V = 1 3 S A B C . S A = 1 3 . a 2 3 4 . a 3 = a 3 4

Đáp án A
Do tam giác ABC đều cạnh a nên có S ∆ A B C = a 2 3 4
⇒ V = 1 3 S A . S ∆ A B C = 1 3 . a 6 . a 2 3 4 = a 2 2 4
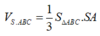
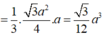

Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AI\)
\( \Rightarrow d\left( {SA,BC} \right) = AI = \frac{{BC\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)