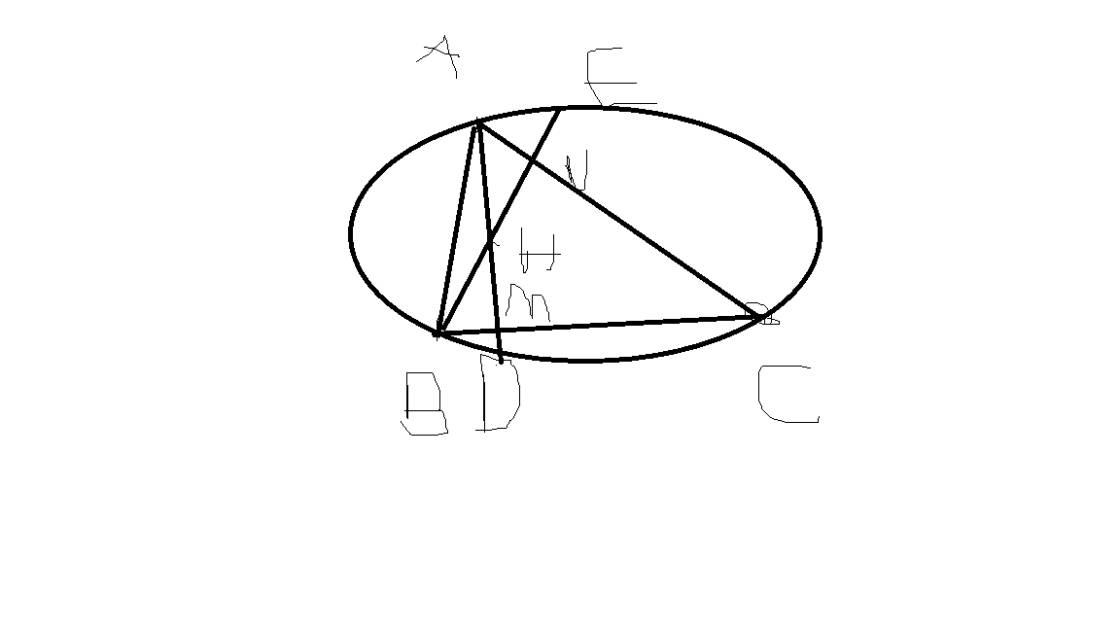
Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). H là trực tâm của tam giác ABC. Từ B kẻ đường thẳng song song với HC. Từ C kẻ đường thẳng song song với HB. Hai đường thẳng này cắt nhau tại D. Hãy chứng minh:
1. Tứ giác ABDC nội tiếp và AD là đường kính của đường tròn (O;R)
2. BAH^ = CAO^
a. Gọi E là giao điểm của BC và HD; G là giao điểm của AE và OH. Chứng minh: G là trọng tâm của tam giác ABC.
b. Cho ABC ^= 60*. Tính diện tích hình quạt tròn COD (ứng với cung nhỏ CD).
4. Nếu OH song song với BC thì tanB.tanC = 3 với B, C là hai góc của tam giác ABC.

a) Ta có: Điểm K đối xứng với điểm F qua AC => FC=KC; AF=AK
=> ΔACF=ΔACK (c.c.c) => ^AFC=^AKC (2 góc tương ứng)
Ta thấy tứ giác ABFC nội tiếp đường tròn tâm O => ^AFC=^ABC.
H là trực tâm của tam giác ABC => CH⊥AB (tại D)
=> ^HCB + ^ABC = 90 (1)
Lại có AH⊥⊥BC => ^LHC + ^HCB = 90 (2)
Từ (1) và (2) => ^ABC=^LHC. Mà ^LHC + ^AHC = 180
=> ^ABC + ^AHC = 180. Do ^ABC=^AFC=^AKC (cmt) => ^AKC + ^AHC= 180
Xét tứ giác AHCK có: ^AKC + ^AHC =180 => Tứ giác AHCK nội tiếp đường tròn (đpcm).
b) AO cắt GI tại Q
Gọi giao điểm của AO và (O) là P = >^ACP=90 => ^CAP+^CPA=90 (*)
Thấy tứ giác ACPB nội tiếp đường tròn (O) => ^CPA=^ABC
Mà ^ABC+^AHC=180=> ^CPA+^AHC=180 (3).
Ta có tứ giác AHCK là tứ giác nội tiếp (cmt) => ^KAI=^CHI
Lại có ΔACF=ΔACK => ^FAC=^KAC hay ^KAI=^GAI => ^GAI=^CHI
Xét tứ giác AHGI: ^GAI=^GHI (=^CHI) (cmt) = >Tứ giác AHGI nội tiếp đường tròn
=> ^AIG+^AHG=180 hay ^AIG + ^AHC=180 (4)
Từ (3) và (4) => ^AIG=^CPA (*)
Từ (*) và (**) => ^CAP+^AIG=900hay ^IAQ+^AIQ=900 => ΔAIQ vuông tại Q
Vậy AO vuông góc với GI (đpcm).
Sai đề kìa