cho hình bình hành ABCD có 2 đường chéo AC,BD cắt nhau tại O thoả mãn góc OAB=góc ODC chứng minh ABCD là hình chữ nhật
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2023
Xét ΔOAD và ΔOCB có
\(\widehat{OAD}=\widehat{OCB}\)
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
Do đó: ΔOAD=ΔOCB
=>AD=BC
\(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này ở vị trí so le trong
nên AD//BC
Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
25 tháng 3 2021
Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB(Hai cạnh đối của hình bình hành ABCD)
\(\widehat{D}=\widehat{B}\)(Hai góc đối của hình bình hành ABCD)
Do đó: ΔAED=ΔCFB(cạnh huyền-góc nhọn)
Suy ra: AE=CF(Hai cạnh tương ứng) và ED=FB(hai cạnh tương ứng)
Ta có: ED+EC=DC(E nằm giữa D và C)
FB+FA=AB(F nằm giữa A và B)
mà AB=DC(Hai cạnh đối của hình bình hành ABCD)
và ED=FB(cmt)
nên EC=FA
Xét tứ giác ECFA có
EC=FA(cmt)
EA=CF(cmt)
Do đó: ECFA là hình bình hành(Dấu hiệu nhận biết hình bình hành)
CM
3 tháng 8 2018
Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: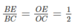 
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).
D
11 tháng 9 2017
gọi góc DAH = góc HAO =góc OAB = x
Xét tam giác OAD cân tại A(....)
=> góc ADH = 90 độ - x (1)
=> góc DOC = 180 độ - 2x (góc ngoài)
_góc ACD=x ( soletrong ...)
Xét tam giác ODC có
góc ODC = 180 độ - góc ACD - góc DOC
=180 độ - 180 độ + 2x -x
= x
=> góc ODC = x (2)
từ (1) và (2) => góc ADC = 90 độ - x + x =90 độ
=> H.B.Hành có 1 góc vg=> đó là Hình Chữ Nhật (dpcm)
AH
Akai Haruma
Giáo viên
22 tháng 12 2020
Lời giải:
Xét tam giác ADH và AOH có:
\(\widehat{DAH}=\widehat{OAH}\) (gt)
\(\widehat{AHD}=\widehat{AHO}=90^0\)
AH chung
\(\Rightarrow \triangle ADH=\triangle AOH(g.c.g)\) (1)
\(\Rightarrow AD=AO\Rightarrow \frac{AD}{AO}=1\)
Xét tam giác ADH và AOK có:
\(\widehat{AHD}=\widehat{AKO}=90^0\)
\(\widehat{DAH}=\widehat{OAB}=\widehat{OAK}\) (gt)
\(\Rightarrow \triangle ADH\sim \triangle AOK(g.g)\Rightarrow \frac{AH}{AK}=\frac{DH}{OK}=\frac{AD}{AO}=1\Rightarrow AH=AK;DH=OK\)
Vì AO là phân giác của \(\widehat{HAB}\) nên theo tính chất đường phân giác thì:
\(\frac{AH}{AB}=\frac{OH}{OB}\)
Trong đó \(OH=DH\) (do (1)) nên \(OH=\frac{1}{2}OD\). Mà \(OD=OB\) theo tính chất hình bình hành
\(\Rightarrow \frac{AH}{AB}=\frac{OH}{OB}=\frac{1}{2}\)
Mà \(AH=AK\Rightarrow AK=\frac{1}{2}AB\Rightarrow AK=KB\)
Tam giác AOB có OK vừa là đường cao vừa là đường trung tuyến nên tam giác AOB cân tại O. Do đó OA=OB hay AC=BD nên ABCD là hình chữ nhật (đpcm).
19 tháng 6 2018
a) \(BE;DF\perp AC\text{ nên }BE//DF\)
\(\Delta BEO=\Delta DFO\) (cạnh huyền - góc nhọn)
=> BE = FD
\(\Rightarrow\Delta BEDF\text{ là }HBH\)
b) \(\Delta BHC~\Delta DKC\) (g.g)
\(\widehat{H}=\widehat{G}=90^o\)
\(\widehat{CBH}=\widehat{CDK}\) (vì 2 góc này kề bù vs 2 góc bằng nhau là \(\widehat{CBA}=\widehat{ADC}\))
\(\Rightarrow\frac{BC}{DC}=\frac{HC}{KC}\)
\(\Rightarrow CB.CK=CH.CD\)
c) Ta có: \(\Delta ABE~\Delta ACH\)
\(\Rightarrow\frac{AB}{AC}=\frac{AE}{AH}\)
\(\Rightarrow AB.AH=AE.AC\)
\(\Leftrightarrow AD.AK=AF.AC\)
\(\Rightarrow AB.AH+AD.AK=AC.\left(AF+AE\right)=AC.2AO=AC^2\)
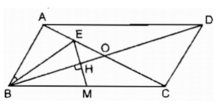
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AB//CD
=>góc OAB=góc OCD
mà góc OAB=góc ODC
nên góc ODC=góc OCD
=>OC=OD
=>AC=BD
Xét hình bình hành ABCD có AC=BD
nên ABCD là hình chữ nhật