cho (O) và một đường thẳng d năm ngoài. P chuyển động trên d. Qua P kẻ hai tiếp tuyến PA, PB tới (O). gọi I là hình chiếu của O lên d. Từ I kẻ hai tiếp tuyến IM, IM tới (O). MN cắt OI tại H.
a) CMR: A, H, B thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
9 tháng 6 2021
1) Trong (O) có CD là dây cung không đi qua (O) và H là trung điểm CD
\(\Rightarrow OH\bot CD\Rightarrow\angle OHI=90=\angle OAI\Rightarrow OHAI\) nội tiếp
Ta có: \(\angle OAI+\angle OBI=90+90=180\Rightarrow OAIB\) nội tiếp
\(\Rightarrow O,H,A,B,I\) cùng thuộc 1 đường tròn
2) Vì IA,IB là tiếp tuyến \(\Rightarrow IB=IA=OA=OB\Rightarrow AOBI\) là hình thoi
có \(\angle OAI=90\Rightarrow AOBI\) là hình vuông
AB cắt OI tại E.Dễ chứng minh được E là trung điểm AB
Ta có: \(AB=\sqrt{OA^2+OB^2}=\sqrt{2}R\Rightarrow AE=\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) bán kính của (AOBI) là \(\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) diện tích của (AOBI) là \(\left(\dfrac{\sqrt{2}}{2}R\right)^2.\pi=\dfrac{1}{2}\pi R^2\)
3) OH cắt AB tại F
Ta có: \(\angle IEF=\angle IHF=90\Rightarrow IEHF\) nội tiếp
\(\Rightarrow OH.OF=OE.OI\) (cái này chỉ là đồng dạng thôi,bạn tự chứng minh nha)
mà \(OE.OI=OB^2=R^2\Rightarrow OF=\dfrac{R^2}{OH}\)
mà H cố định \(\Rightarrow\) F cố định \(\Rightarrow AB\) đi qua điểm F cố định 
28 tháng 4 2023
a: ΔOAB cân tại O
mà OH là trung tuyến
nên OH vuông góc AB
góc OHI=góc OMI=góc ONI=90 độ
=>O,H,M,I,N cùng thuộc đường tròn đường kính OI
=>ĐPCM
b: Xét (O) co
IM,IN là trung tuyến
=>IM=IN
mà OM=ON
nên OI là trung trực của MN
=>OI vuông góc MN tại J
Xet ΔIJK và ΔIHO có
góc IJK=góc IHO
góc JIK chung
=>ΔIJK đồng dạng với ΔIHO
=>IJ/IH=IK/IO
=>IK*IH=IJ*IO
c: sin MIO=OM/OI=1/2
=>góc MIO=30 độ
=>góc MIN=60 độ
\(IM=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(S_{IMN}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3\cdot R^2\cdot\sqrt{3}}{4}\)
10 tháng 5 2023
a: góc IMO+góc INO=180 độ
=>IMON nội tiếp
b: Xét ΔINH và ΔIKN có
góc INH=góc IKN
góc NIH chung
=>ΔINH đồng dạng với ΔIKN
=>IN^2=IH*IK
HS
3 tháng 4 2016
Ta có : góc AMO = góc ANO = 900 (t/c tiếp tuyến)
Mặt khác I là tđ BC => OI vuông góc BC (t/c đường kính và dây) => góc AIO = 900
=> 5 điểm A, M, O, I, N cùng nằm trên một đường tròn
Ta có góc MAI = góc MNI (AMIN nt), mà góc EBI = góc MAI (đồng vị, do AM // BE) => góc MNI = góc EBI hay góc ENI = góc EBI
=> Tứ giác NBEI nội tiếp => góc BNE = góc BIE. Mà góc BNE = góc BCM (cùng chắn cung MB trong (O))
=> góc BIE = góc BCM => IE // CM
CM
10 tháng 8 2019
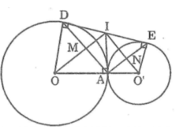
Trong đường tròn (O) ta có OI là tia phân giác của góc AID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE (tính chất hai tiếp tuyến cắt nhau)
=> IO ⊥ IO’ (tính chất hai góc kề bù)
Suy ra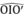 
=
90
°
hay 
=
90
°
Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác ADI cân tại I
Tam giác cân AID có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID
Suy ra: IO ⊥ AD hay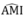 
=
90
°
Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AEI cân tại I
Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO’ cũng là đường cao của tam giác AIE
Suy ra: IO’ ⊥ AE hay 
=
90
°
Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.