Cho ΔABC, góc A = α (0o < α < 900). Vẽ các đường cao BD và CE.
a) Chứng minh: DE = BC . cosA.
b) Gọi M là trung điểm BC. Tính α để ΔMDE đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
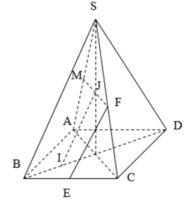
Gọi I,J lần lượt là trung điểm cạnh BC và SA
Ta có A C ⊥ S B D , EI // AC, MJ//AC => E I ⊥ ( S B D ) , M J ⊥ ( S B D )
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
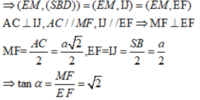

Đáp án C
Phương pháp:
- Gắn hệ trục tọa độ Oxyz, tìm tọa độ các điểm E, M.
- Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin α = n → . u → n → . u →
Cách giải:
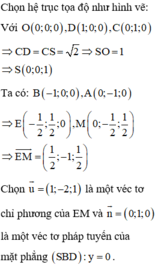
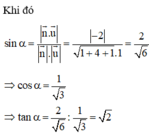

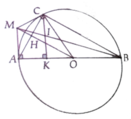
a, HS tự làm
b, HS tự làm
c, IK = 1 2 CK = 1 2 AC.sinα = R.cosα.sinα
d, Giả sử BI cắt AM tại N. Vì IK//AM => MO = OP
=> 1 O I 2 = 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => M ≡ N
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>DE/BC=AD/AB=cosA
=>DE=BC*cosA
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp đường tròn đường kính BC
=>M là tâm đường tròn ngoại tiếp tứ giác BEDC
ΔMDE đều khi MD=ME=DE
=>MD=BC*cosA
mà MD=BC/2
nên BC/2=BC*cosA
=>BC*cosA-BC/2=0
=>\(BC\cdot\left(cosA-\dfrac{1}{2}\right)=0\)
=>\(cosA=\dfrac{1}{2}\)
=>\(\widehat{A}=60^0\)