Vận tốc riêng của một canô là 24km/giờ, vận tốc dòng nước là 3km/giờ. Với khoảng thời gian để canô chạy ngược dòng được 35km thì canô chạy xuối dòng được bao nhiêu km?
A: 30km
B: 54km
C: 45km
D: 35km
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có : vận tốc chạy xuôi dòng của ca nô là 21+3=24 km/h
vận tốc chạy ngược dòng của ca nô là 21−3=18 km/h
thời gian của ca nô chạy ngược dòng 30km là 3018=53 giờ
⇒ thời gian để ca nô chạy ngược dòng 30km thì ca nô chạy xuôi dòng được 53.24=40km/h
vậy thời gian để ca nô chạy ngược dòng 30km thì ca nô chạy xuôi dòng được 40km/h
Câu hỏi của Dao Thuy Trang - Toán lớp 7 - Học toán với OnlineMath

Đáp án:vận tốc ca nô là 43 km/h và vận tốc nước là 3 km/h
Giải thích các bước giải:
Gọi vận tốc xuôi dòng của ca nô là x (km/h) và ngược dòng là y (km/h)
(x>y>0)
1 giờ rưỡi= 1,5 giờ
Ta có hệ pt:
{1.x+2.y=1261,5x+1,5y=129⇒{x=46(km/h)y=40(km/h){1.x+2.y=1261,5x+1,5y=129⇒{x=46(km/h)y=40(km/h)
Ta có x=ca nô + nước; y= ca nô - nước
=> vận tốc riêng của ca nô là: x+y2=43(km/h)x+y2=43(km/h)
Vận tốc dòng nước là 3 km/h

a)
Ta ký hiệu canô là (1), nước là (2), bờ sông là (3)
Áp dụng công thức cộng vận tốc: 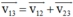 (0,25 đ)
(0,25 đ)
Khi canô xuôi dòng: 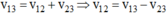 (0,50 đ)
(0,50 đ)
Mà 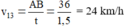 (0,25đ)
(0,25đ)
Vậy vận tốc của canô đối với nước: v 12 = 24 – 6 = 18 km/h (0,25đ)
b) Khi ca nô đi ngược dòng:
v 13 = v 12 - v 23 (0,25đ)
= 18 - 6 = 12 km/h (0,25đ)
Vậy thời gian ngược dòng của canô: 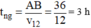 (0,25đ)
(0,25đ)

a) Gọi: (0,25 điểm)
(1): canô (2): nước (3): bờ sông
Áp dụng công thức cộng vận tốc: 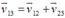 (0,25 điểm)
(0,25 điểm)
Khi canô xuôi dòng:
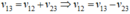 (0,25 điểm)
(0,25 điểm)
Mà 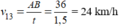 (0,25 điểm)
(0,25 điểm)
Vậy vận tốc của canô đối với nước: v 12 = 24 – 6 = 18 km/h (0,25 điểm)
b) khi ca nô đi ngược dòng: v 13 = v 12 - v 23 (0,25 điểm)
= 18 - 6 = 12 km/h (0,25 điểm)
Vậy thời gian ngược dòng của canô: 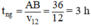 (0,25 điểm)
(0,25 điểm)

Gọi \(\left(1\right)\) : canô
\(\left(2\right)\) : nước
\(\left(3\right)\) : bờ
Vận tốc khi xuôi dòng là : \(40:1=40\left(km/h\right)\)
Vận tốc khi ngược dòng là : \(40:1,25=32\left(km/h\right)\)
Ta có : \(\overrightarrow{V_{13}}=\overrightarrow{V_{12}}+\overrightarrow{V_{23}}\)
\(TH_1:\) \(\overrightarrow{V_{12}}\uparrow\uparrow\overrightarrow{V_{23}}\) \(\Rightarrow V_{13}=V_{12}+V_{23}=40\)
\(TH_2:\overrightarrow{V_{12}}\uparrow\downarrow\overrightarrow{V_{23}}\Rightarrow V_{13}=V_{12}+V_{23}=32\)
Từ 2TH, ta suy ra : \(\left\{{}\begin{matrix}V_{12}=36\left(km/h\right)\\V_{23}=4\left(km/h\right)\end{matrix}\right.\)
Vậy ...
Gọi vận tốc cano cần tìm là x(km/h)
Vận tốc cano xd là x + y(km/h)
Khi nd là x-y(km/h)
Cả quãng đường xuôi lẫn ngực dòng là 40 nên ta có
\(v_{xd}.t_1=s \Leftrightarrow\left(x+y\right).1=40\Leftrightarrow x+y=40\\ v_{nd}t_2=s\Leftrightarrow\left(x-y\right).\dfrac{5}{4}=40\Leftrightarrow x-y=32\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=36\\y=4\end{matrix}\right.\)
C : 45 km
...............
..........
Để câu trả lời của bạn nhanh chóng được duyệt và hiển thị, hãy gửi câu trả lời đầy đủ và không nên: