cho hình thang ABCD, AB//CD. M là trung điểm của CD, I là giao điểm của AM và BD; K là giao điểm của BM và AC. gọi O là giao điểm AC và BD.MO cắt AB tại N; BO cắt BC tại S. CMR: N là trung điểm của AB. A;D;S thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1 2022
D là đáp án đúng (do I là giao điểm AC và BM \(\Rightarrow I=\left(SAC\right)\cap\left(SBM\right)\)
\(\Rightarrow SI=\left(SAC\right)\cap\left(SBM\right)\)
18 tháng 2 2021
Xét ΔDEM và ΔBEA có
\(\widehat{DEM}=\widehat{BEA}\)(hai góc đối đỉnh)
\(\widehat{DME}=\widehat{BAE}\)(hai góc so le trong, DM//AB)
Do đó: ΔDEM\(\sim\)ΔBEA(g-g)
Suy ra: \(\dfrac{EM}{EA}=\dfrac{DM}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(1)
Xét ΔMFC và ΔBFA có
\(\widehat{MFC}=\widehat{BFA}\)(hai góc đối đỉnh)
\(\widehat{MCF}=\widehat{BAF}\)(hai góc so le trong, AB//MC)
Do đó: ΔMFC\(\sim\)ΔBFA(g-g)
Suy ra: \(\dfrac{FM}{FB}=\dfrac{CM}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)(2)
Ta có: M là trung điểm của CD(gt)
nên CM=DM(3)
Từ (1), (2) và (3) suy ra \(\dfrac{EM}{EA}=\dfrac{FM}{FB}\)
Xét ΔMAB có
E\(\in\)AM(gt)
\(F\in BM\)(gt)
\(\dfrac{EM}{EA}=\dfrac{FM}{FB}\)(cmt)
Do đó: EF//AB(Định lí Ta lét đảo)
13 tháng 6 2023
2: Xét ΔEAB và ΔEMD có
góc EAB=góc EMD
góc EBA=góc EDM
=>ΔEAB đồng dạng với ΔEMD
=>EA/EM=AB/MD=AB/MC
=>ME/EA=MC/AB
Xét ΔFMC và ΔFBA có
góc FMC=góc FBA
góc MFC=góc BFA
=>ΔFMC đồng dạng với ΔFBA
=>FM/FB=MC/BA=ME/MA
=>EF//AB
=>FE/AB=MF/MB=1:(1+BF/MF)=1:(1+AB/CD)=1:(AB+CD)/CD
=CD/(AB+CD)
B1
31 tháng 8 2017
1]
a]
Ta có:
AI/IM = AB/DM
BK/KM = AB/MC
Do DM =MC
=> AI/IM = BK/KM
=> IK//AB
b]
IE/DM = AI/AM
KF/MC = BK/BM
Mà AI/AM = BK/BM (do IK//AB)
=> IE/DM = KF/MC mà DM=MC
=> IE = KF
2]
a}
Ta có:
AE/EK = AB/DK
BF/FI = AB/CI
Do ABID và ABCK là h..b.hành
=> CK=DI =AB
=> DK = CI = CD -AB
=> AE/EK = NF/FI
=> EF//AB
b}
Ta có EF/CK =AF/AC = AB/CD
=> EF.CD = CK.AB = AB^2 (do CK =AB)
3]
a}
Ta có:
MB/MF = MC/MA (Xét BC//AF)
ME/MB = MC/MA (Xét CE//AB)
=> MB/MF = ME/MB
=> MB^2 = ME.MF
b}
BM/MF = MC/AC (Xét BC//AF)
BM/ME = AM/AC (Xét CE//AB)
=> BM/MF + BM/ME = MC/AC + AM/AC =1
=> BM/MF + BM/ME =1
=> 1/BF+1/BE=1/BM
H9
HT.Phong (9A5)
CTVHS
6 tháng 2 2023
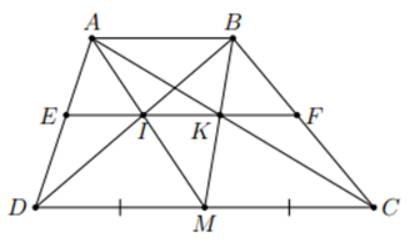
a) Vì AB // CD áp dụng định lý Ta-lét ta có:
\(\dfrac{IM}{IA}\)=\(\dfrac{MD}{AB}\)
\(\Rightarrow\) \(\dfrac{IM}{IA}\)=\(\dfrac{KM}{KB}\) (Vì MC = MD)
\(\dfrac{KM}{KB}\)=\(\dfrac{MC}{AB}\)
Do đó theo định lý Ta-lét đảo ta có IK // AB
Vì IK // AB // CD nên theo định lý Ta-lét :
\(\dfrac{IE}{DM}\)=\(\dfrac{AI}{AM}\)=\(\dfrac{BI}{BD}\)=\(\dfrac{IK}{DM}\)=> EI = IK
Tương tự ta có FK =IK nên ta có EI = IK = KF
5 tháng 3 2022
a. -Xét △ABH có: AB//DM (gt)
\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{DM}\) (định lí Ta-let)
Mà \(DM=\dfrac{1}{2}CD\) (M là trung điểm CD).
\(\Rightarrow\dfrac{AH}{HM}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)
b. Sửa đề: C/m HK//AB.
-Xét △ABK có: AB//CM (gt)
\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{CM}\) (định lí Ta-let)
Mà \(CM=\dfrac{1}{2}CD\) (M là trung điểm CD).
\(\Rightarrow\dfrac{AK}{KC}=\dfrac{AB}{\dfrac{1}{2}CD}=\dfrac{2AB}{CD}\)
-Xét △ABM có: \(\dfrac{AH}{HM}=\dfrac{AK}{KC}\left(=\dfrac{2AB}{CD}\right)\)
\(\Rightarrow\)HK//AB.
c. -Xét △ABM có: HK//AB (cmt).
\(\Rightarrow\dfrac{AB}{HK}=\dfrac{AM}{HM}\) (định lí Ta-let).
\(\Rightarrow\dfrac{AB-HK}{HK}=\dfrac{AM-HM}{HM}\)
\(\Rightarrow\dfrac{AB}{HK}-1=\dfrac{AH}{HM}\)
Mà \(\dfrac{AH}{HM}=\dfrac{2AB}{CD}\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{HK}=\dfrac{2AB}{CD}\)
\(\Rightarrow\dfrac{a}{HK}=\dfrac{2a}{b}\)
\(\Rightarrow HK=\dfrac{b}{a}\)
CM
27 tháng 12 2019
a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
Xét tam giác vuông AHB, ta có :
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)