Cho tam giác ABC vuông ở A. Giả sử D là một điểm trên cạnh huyền BC và E, F lần lượt là hình chiếu của D trên cạnh AB, AC. Chứng minh rằng AE.EB + AF.FC = BD.DC
Ai giúp mình với. Mình đang cần nhanh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

Tứ giác AEHF là hình chữ nhật (có 3 góc vuông) \(\Rightarrow HE=AF\)
Áp dụng định lý Pitago trong tam giác vuông AFH:
\(AH^2=AF^2+HF^2=HE^2+HF^2\)
Áp dụng hệ thức lượng trong tam giác vuông AHB với đường cao HF:
\(HF^2=AF.FC\)
Tương tự:
\(HE^2=AE.EB\)
\(\Rightarrow AH^2=HE^2+HF^2=AE.EB+AF.FC\) (đpcm)

SABC = SDEFG + SBED + SGEF +SADG
SABC = SDEFG khi d tịnh tiến trùng với A
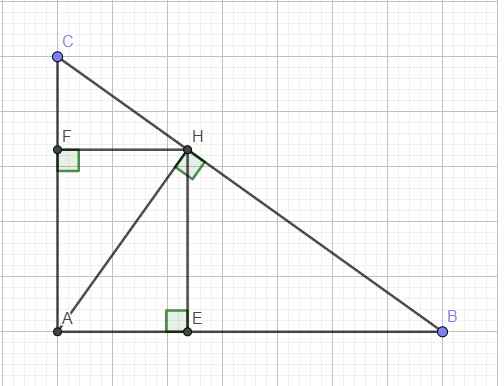
Tứ giác AEDF có \(\widehat{A}=\widehat{E}=\widehat{F}=90\)nê AEDF là hình chữ nhật.
\(\Rightarrow\hept{\begin{cases}AE=DF\\AF=DE\end{cases}\Rightarrow\hept{\begin{cases}AE.EB=DF.EB\\\end{cases}}}\)
thế làm sao nó ra được BD.DC ?