thường ngày đến công trường, bác hoan dùng 1 chiếc thang lớn dựng lên 1 bức tường cao 6m. khi đặt chân thang cách chân tường 1,5m thì vừa dựng thang lên đúng mặt trên bức tường. hôm nay bác hoan chỉ có 1 chiếc thang nhỏ dài bằng 2/3 chiếc thang lớn. để đảm bảo an toàn bác đặt chân thang cách chân tường 1m. hỏi khi dựng chiếc thang nhỏ lên thì điểm cao nhất của thang cách mặt trên bức tường bao nhiêu mét?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

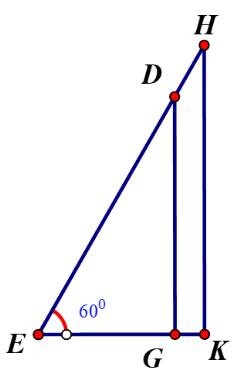
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.

( Hình ảnh chỉ có tính chất minh họa )
Áp dụng định lý Pytago vào tam giác ABC, ta có:
AB2 + AC2 = BC2
=> AB2 + 32 = 52
=> AB2 + 9 = 25
=> AB2 = 25 - 9
=> AB2 = 16
=> AB = 4m
nhớ tk cho mk nha
bạn bị hâm à?đến bạn còn trả biết làm mà bạn đi bảo mình làm là sao? hỏi bạn khác đi.

theo ta thấy thì chân tường có 90o=> hình tạo ra từ chân tường nhà của bác An và cái thang là hình tam giác vuông, vậy ta có hình như sau:
gọi số mét cách từ mặt đất lên mái nhà là x
áp dụng tính chất định lý pi-ta-go, ta có:
32+x2=52
=>9+x2=25
=>x2=16
=>x=4
Vậy số mét cách từ mặt đất lên mái nhà của bác An là 4m

Vẽ tam giác ABC, BC=2,5m, AC=6,5m. ABC vuông tại B
Dịnh lí Pitago: AB=\(\sqrt{AC^2-BC^2}\) =6m
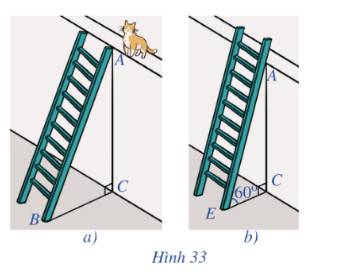
Gọi tam giác tạo thành là tam giác ABC
Với chiếc thang là cạnh huyền AC, khoảng cách của chân thang và chân tường là BC và chiều cao của bức tường là AB:
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{1,5^2+6^2}\approx6,2\left(m\right)\)
Độ dài của chiếc thang nhỏ:
\(A'C'=\dfrac{2}{3}\cdot AC=\dfrac{2}{3}\cdot6,2\approx4,13\left(m\right)\)
Áp dụng định lý Py-ta-go ta tìm được độ cao mà thang đặt đến:
\(A'B'=\sqrt{A'C'^2-B'C'^2}=\sqrt{4,13^2-1^2}\approx4\left(m\right)\)
Điểm cao nhất của thang cách mặt bước tường là:
\(AB-A'B'=6-4=2\left(m\right)\)
Vậy....