Cho điểm M nằm bên trong (O;R). Qua M kẻ 2 dây AB và CD vuông góc với nhau. CMR: Nếu M cố định, 2 dây AB và CD thay đổi nhưng vẫn vuông góc với nhau thì AB2 + CD2 luôn không thay đổi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

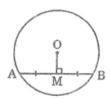
* Cách dựng
- Dựng đoạn OM
- Qua M dựng đường thẳng vuông góc với OM cắt O tại A và B.
Nối A và B ta được dây cần dựng
*Chứng minh
Ta có: OM ⊥ AB ⇒ MA = MB

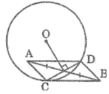
Ta có: OI ⊥ CD (gt)
Suy ra: IC = ID (đường kính dây cung)
Mà: IA = IB (gt)
Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

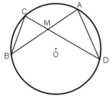
TH1: M nằm trong đường tròn.
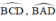 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 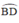
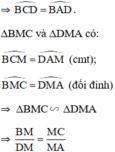
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
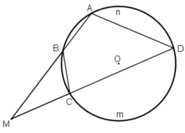
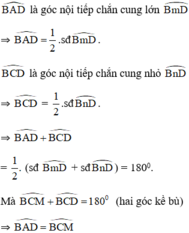
ΔMBC và ΔMDA có:
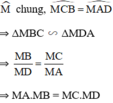
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.

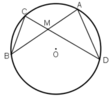
TH1: M nằm trong đường tròn.
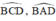 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 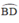
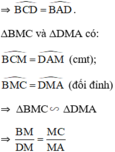
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
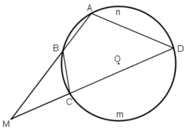
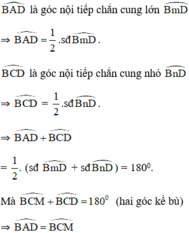
ΔMBC và ΔMDA có:
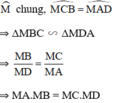
Hạ \(OH\perp AB\), \(OK\perp CD\). Dễ thấy tứ giác OHMK là hình chữ nhật \(\Rightarrow HK=OM\)
Lại có \(AB^2=4HB^2=4\left(OB^2-OH^2\right)=4R^2-4OH^2\) (1)
và \(CD^2=4CK^2=4\left(OC^2-OK^2\right)=4R^2-4OK^2\) (2)
Từ (1) và (2), suy ra \(AB^2+CD^2=8R^2-4\left(OH^2+OK^2\right)\) \(=8R^2-4HK^2=8R^2-4OM^2\) không đổi, đpcm.