Xác định bán kính của Ca nếu khối lượng riêng của Ca là 1,55 g/cm3 và nguyên tử khối là 40,08. Biết rằng trong tinh thể các nguyên tử Ca chiếm 74% thể tích trong tinh thể?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
bài giải đây nha!
LL
20 tháng 1 2019
bài 2 : Để so sánh số nguyên tử thì mình có thể thông qua số mol vì
N = n.N0 (N0 là số Avogadro)
n = m/M = DV/M
n(Pt) = 21.45 x 1/195
n(Au) = 19.5 x 1/197
Bạn tự bấm máy tính để ra kq nhe :D
LL
20 tháng 1 2019
bài 1 : thể tích 1 mol Ca
V=40.08∗0.741.55=6.02∗1023∗4/3∗pi∗R3V=40.08∗0.741.55=6.02∗1023∗4/3∗pi∗R3
trong đó V=m/d=4/3∗pi∗R3V=m/d=4/3∗pi∗R3
còn 6.02∗10236.02∗1023 là số lượng nguyên tử của 1 mol
máy tỉnh bỏ túi solve hoặc giải pt bằng tay là ra R=1.96∗10−8R=1.96∗10−8
với Cu cậu làm tương tự là ra
TP
13 tháng 8 2021
Thể tích của nguyên tố R: \(V_1=\dfrac{M}{d}\)
Giả thiết rằng, trong tinh thể R các nguyên tử là những hình cầu chiếm 74%
=> Thể tích của tất cả nguyên tử là:\(V_2=V_1.0,74\)
Thể tích của từng nguyên tử là: \(V_3=\dfrac{V_2}{6,023.10^{23}}\)
Mặt khác: \(V_3=\dfrac{4}{3}.pi.R^3=3,178.10^{-23}cm^3\)
\(\Rightarrow M=\dfrac{3,178.10^{-23}.6,023.10^{23}.1,55}{0,74}=40\)
=> R là Ca
8 tháng 2 2019
Khối lượng riêng của nguyên tử là:
D = 19,36.100/74 = 26,16(g/ cm 3 )
Khối lượng của 1 mol nguyên tử :
M = V.D.N = 4/3π r 3 .D.N = 4/3. 3,14. 1 , 44 . 10 - 8 3 .26,16. 6,022. 10 23 ≈ 197 (g/mol)
5 tháng 8 2019
Nguyên tử khối là 197.
ta có : nguyên tử khối ≈số khối = P+N
số proton = 197 – 118 = 79
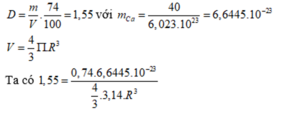
\(V_{1.mol.Ca\left(tinh.thể\right)}=\dfrac{40,08g}{1,55g/cm^3}=25,858cm^3\)
\(V_{thực.sự.1mol.Ca}=25,858.\dfrac{74}{100}=19,135cm^3\)
\(\Rightarrow V_{1.nguyên.tử.Ca}=\dfrac{19,135}{6,023.10^{23}}=3,18.10^{-23}cm^3\)
Giả sử nguyên tử Ca là khối cầu thì: \(V=\dfrac{4}{3}\pi R^3\Rightarrow R=\sqrt[3]{\dfrac{3V}{4\pi}}\)
\(R_{Ca}=\sqrt[3]{\dfrac{3.3,18.10^{-23}}{4.3,14}}=1,97.10^{-8}cm\) hay \(1,97\) \(A^o\)