Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Δ=(2m-1)^2-4*2*(m-1)
=4m^2-4m+1-8m+8
=4m^2-12m+9=(2m-3)^2>=0
=>PT luôn có 2 nghiệm
4x1^2+4x2^2+2x1x2=0
=>4[(x1+x2)^2-2x1x2]+m-1=0
=>4[(-2m+1)^2/4-2*(m-1)/2]+m-1=0
=>(2m-1)^2-4(m-1)+m-1=0
=>4m^2-4m+1-3m+3=0
=>4m^2-7m+4=0
=>\(m\in\varnothing\)
a: Khi m=2 thì pt sẽ là \(x^2-8x-9=0\)
=>x=9 hoặc x=-1
b: \(\text{Δ}=\left(2m+4\right)^2-4\left(-2m-5\right)\)
\(=4m^2+16m+16+8m+20=4m^2+24m+36\)
\(=4\left(m^2+6m+9\right)=4\left(m+3\right)^2>=0\)
Để phương trình có hai nghiệm phân biệt thì m+3<>0
hay m<>-3
Theo đề, ta có: \(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
\(\Leftrightarrow\sqrt{\left(2m+4\right)^2-4\left(-2m-5\right)}=2\)
\(\Leftrightarrow\sqrt{4m^2+16m+16+8m+20}=2\)
\(\Leftrightarrow4m^2+24m+36=4\)
\(\Leftrightarrow m^2+6m+9=1\)
=>m+3=1 hoặc m+3=-1
=>m=-2 hoặc m=-4
1) Thay m=2 vào (1), ta được:
\(x^2-2\cdot3x+16-8=0\)
\(\Leftrightarrow x^2-6x+8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
Vậy: Khi m=2 thì (1) có hai nghiệm phân biệt là: \(x_1=2\); \(x_2=4\)
b) Ta có: \(\Delta=4\cdot\left(2m-1\right)^2-4\cdot1\cdot\left(8m-8\right)\)
\(\Leftrightarrow\Delta=4\cdot\left(4m^2-4m+1\right)-4\left(8m-8\right)\)
\(\Leftrightarrow\Delta=16m^2-16m+4-32m+32\)
\(\Leftrightarrow\Delta=16m^2-48m+36\)
\(\Leftrightarrow\Delta=\left(4m\right)^2-2\cdot4m\cdot6+6^2\)
\(\Leftrightarrow\Delta=\left(4m-6\right)^2\)
Để phương trình có hai nghiệm phân biệt thì \(\left(4m-6\right)^2>0\)
mà \(\left(4m-6\right)^2\ge0\forall m\)
nên \(4m-6\ne0\)
\(\Leftrightarrow4m\ne6\)
hay \(m\ne\dfrac{3}{2}\)
Vậy: Để phương trình có hai nghiệm phân biệt thì \(m\ne\dfrac{3}{2}\)
a)thay m=1 vào pt ta có
\(x^2+4x=0\)
<=> \(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b) thay x=2 vào pt ta có: 13+m=0
<=>m=-13
thay m=-13 vào pt ta có
\(x^2+4x-12=0\)
<=>(x-2)(x+6)=0
<=>\(\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)\(\)
vậy với m=-13 thì nghiệm còn lại là x=-6
c) để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>16-4m-4>0
<=>3-m>0
<=>m<3
áp dụng định lí Vi-ét ta có\(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=m+1\end{matrix}\right.\)
theo đề bài ta có \(x_1^2+x_2^2=10\)
<=>\(\left(x_1+x_2\right)^2-2x_1x_2=10\)
<=>16-2m-2=10
<=>2-m=0
<=>m=2(nhận)
vậy với m=2 thì pt có 2 nghiệm pb thỏa yêu cầu đề bài.
PT x 2 − 2 m + 1 x + m 2 − 1 = 0 ( 1 ) có 2 nghiệm phân biệt x 1 , x 2
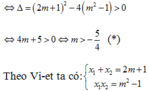
Theo Vi-et ta có: x 1 + x 2 = 2 m + 1 x 1 x 2 = m 2 − 1
Ta có: x 1 2 + x 2 2 + 8 x 1 x 2 = x 1 + x 2 2 + 6 x 1 x 2 = 2 m + 1 2 + 6 m 2 − 1
= 10 m 2 + 2 5 m + 1 25 − 27 5 = 10 m + 1 5 2 − 27 5
⇒ x 1 2 + x 2 2 + 8 x 1 x 2 ≥ − 27 5
Dấu ‘=’ xảy ra khi m = − 1 5 (thỏa mãn (*))
Vậy x 1 2 + x 2 2 + 8 x 1 x 2 đạt giá trị nhỏ nhất khi m = − 1 5
Đáp án cần chọn là: C
3:
\(\Delta=\left(2m-1\right)^2-4\left(-2m-11\right)\)
=4m^2-4m+1+8m+44
=4m^2+4m+45
=(2m+1)^2+44>=44>0
=>Phương trình luôn có hai nghiệm pb
|x1-x2|<=4
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< =4\)
=>\(\sqrt{\left(2m-1\right)^2-4\left(-2m-11\right)}< =4\)
=>\(\sqrt{4m^2-4m+1+8m+44}< =4\)
=>0<=4m^2+4m+45<=16
=>4m^2+4m+29<=0
=>(2m+1)^2+28<=0(vô lý)
đạt giá trị nhỏ nhất
a: Khi m=1 thì (1) sẽ là 2x^2-3x-5=0
=>2x^2-5x+2x-5=0
=>(2x-5)(x+1)=0
=>x=5/2 hoặc x=-1
b: 2x1(2+x2)+4x2(1-x1)+8x1x2=2015
=>4x1+4x2+8x1x2=2015
=>4*(x1+x2)+8x1x2=2015
=>4*(2m+1)/2+8*(-m-4)/2=2015
=>4m+2-4m-16=2015
=>-14=2015(loại)