tô 6 mặt của hình lập phương bằng 5 màu khác nhau. Một màu được dùng để tô cho 2 mặt còn mỗi màu trong 4 màu còn lại dùng để tô cho một mặt. Hỏi có bao nhiêu cách tô hình lập phương? Hai hình được coi là giống nhau nếu chúng nhận được từ nhau bằng các phép quay hoặc phép lật.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 9 2019
Cứ 2 mặt kề nhau thì chung 1 cạnh ( cần vẽ hình ra cho dễ hình dung ) nên 1 cạnh chung đó được tô màu đen thì cả 2 mặt đều có ít nhất 1 cạnh màu đen
Vì hình lập phương có 6 mặt nên cần ít nhất 6 : 2 = 3 cạnh màu đen
CM
3 tháng 1 2017
Cứ 2 mặt kề nhau thì chung 1 cạnh ( cần vẽ hình ra cho dễ hình dung ) nên 1 cạnh chung đó được tô màu đen thì cả 2 mặt đều có ít nhất 1 cạnh màu đen
Vì hình lập phương có 6 mặt nên cần ít nhất 6 : 2 = 3 cạnh màu đen
CM
9 tháng 9 2017
Chọn D
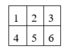
+ Tô màu ô vuông số 2: có C 3 2 cách chọn 2 trong 3 màu, có C 4 2 cách tô 2 màu đó lên 4 cạnh. Vậy có C 3 2 C 4 2 = 18cách.
+ Tô màu ô vuông số 1,5,3: có C 2 1 cách chọn màu còn lại, có C 3 2 cách tô màu còn lại lên 3 cạnh còn lại của 1 hình vuông. Vậy có ( C 2 1 C 3 2 ) 3 = 6 3 cách
+ Tô màu ô vuông số 4,6: Mỗi 1 hình vuông có 2 cách tô màu. Vậy có 2 2 = 4cách.
Vậy có 18. 6 3 .4 = 15552 cách thỏa mãn.
CM
9 tháng 12 2017
Đáp án A
TH1: 4 cạnh với 4 màu khác nhau, có A 6 4 = 360 cách.
TH2: 4 cạnh với 3 màu khác nhau, vì 2 cạnh giống màu không được kề nhau nên có 2 cách đặt vị trí cho 2 giống màu (đặt ở vị trí đối diện nhau). Tiếp theo, có 2! cách cho 2 màu còn lại. Vậy có C 6 3 . 3 .2.2 ! = 240
TH3: 4 cạnh với 2 màu khác nhau (giả sử xanh và đỏ), có 2 cách tô (AB=CD=xanh và AD=BC=đỏ/ hoặc AB=CD=đỏ và AD=BC=xanh) Trong trường hợp này có C 6 2 . 2 = 30 cách.
Vậy có tất cả 360 + 240 + 30 = 630 cách.
CM
10 tháng 8 2019
Đáp án D
Chú ý 4 cạnh khác nhau
Có C 6 4 cách chọn 4 màu khác nhau. Từ mỗi bộ 4 màu thì có 4 ! = 24 cách tô màu khác nhau
Có C 6 3 cách chọn 3 màu khác nhau. Từ mỗi bộ 3 màu, có 4.3 = 12 cách tô
Có C 6 2 cách chọn 2 màu khác nhau khi đó có: 2.1 = 2 cách tô
Tổng cộng: 24. C 6 4 + 4.3 C 6 3 + 2. C 6 2 = 630 cách
hình như bài nỳ là lp 5
Đáp án: có 55 cách tất cả trong các phương án phối màu.
1/ Nếu chỉ dùng 3 màu: có 10 cách
2/ Nếu dùng đúng 4 màu: có 30 cách
3/ Nếu dùng hết 5 màu: có 15 cách