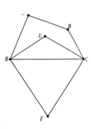
Tứ giác ABCD có \(\widehat{A}\)= 1100 , \(\widehat{B}\)= 1000
CÁC TIA PHÂN GIÁC CỦA GÓC C VÀ GÓC B CẮT NHAU TẠI I. CÁC ĐƯỜNG PHÂN GIÁC CỦA GÓC NGOÀI TẠI CÁC ĐỈNH GÓC C VÀ GÓC D CẮT NHAU TẠI E. TÍNH GÓC CID, GÓC CED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo tại đây:
Bài 8 Sách bài tập - trang 80 - Toán lớp 8 | Học trực tuyến
Bạn chú ý cái đường link rồi sửa thành h là OK hết chỗ nói nha.Hoặc là ib với mik rồi mik cho:3

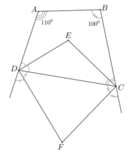
Trong tứ giác ABCD, ta có: ∠ A + ∠ B + ∠ C + ∠ D = 360 °
⇒ ∠ C + ∠ D = 360 ° - ( ∠ A + ∠ B) = 360 ° – ( 110 ° + 100 ° ) = 150 °
Do DE và CE lần lượt là tia phân giác của góc 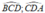
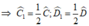
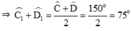
Trong ΔCED ta có:
∠ CED = 180o – ∠ C 1 + ∠ D 1 = 180 ° - 75 ° = 105 °
DE ⊥ DF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ EDF = 90 °
CE ⊥ CF (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ ECF = 90 °
Trong tứ giác CEDF, ta có: ∠ DEC + ∠ EDF + ∠ DFC + ∠ ECF = 360 °
⇒ ∠ DFC = 360 ° - ( ∠ DEC + ∠ EDF + ∠ ECF) = 360 ° - 105 ° - 90 ° - 90 ° = 75 °

a) Sử dụng tính chất dãy tỉ số bằng nhau. A ^ = 144 0 , B ^ = 108 0 , C ^ = 72 0 , D ^ = 36 0
b) Sử dụng tổng ba góc trong tam giác tính được C E D ^ = 126 0 .
Chú ý hai phân giác trong và ngoài tại mỗi góc của một tam giác thì vuông góc nhau, cùng với tổng bốn góc trong tứ giác, ta tính được C F D ^ = 54 0