(0) và dg tròn (0') tiếp xúc ngoài tại A kẻ tt chung ngoài (BC) B thuộc (0) C thuộc (0') tt chung trong tai A cắt tt chung ngoài BC ở I a) CM IB=IA=IC b) CM tam giác BAC VG tại A c) CM OIO' = 90°
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
15 tháng 7 2020
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC .
Tam giác ABC có đường trung tuyến \(AI=\frac{1}{2}BC\)nên là tam giác vuông
Vậy \(\widehat{BAC}=90^o\left(đpcm\right)\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên :
\(\widehat{OIO'}=\widehat{OIA}+\widehat{O'IA}=\frac{1}{2}\widehat{AIB}+\frac{1}{2}\widehat{AIC}=\frac{1}{2}\left(\widehat{AIB}+\widehat{AIC}\right)\)
Vậy : \(\widehat{OIO'}=90^o\)
c) \(\Delta OIO'\) vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9 . 4 = 36
=> IA = 6 ( cm )
Vậy BC = 2 . IA = 2 . 6 = 12 (cm)
LM
Lê Minh Vũ
CTVHS
9 tháng 5 2021
) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
9 tháng 5 2021
Bài làm
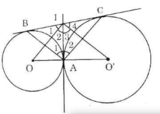
a) Ta thấy: BC là tiếp tuyến chung ngoài và tiếp tuyến chung trong của hai đường tròn (O') và (O) cắt nhau tại I
=> CI = IA = IB (theo tính chất hai tiếp tuyến cắt nhau)
Xét tam giác ABC có: IA = 1/2BC
=> Tam giác ABC vuông tại A
Do đó: góc BAC = 90o (đpcm)
b) Ta thấy: O'I là tia phân giác của CO'O (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IO'O}=\frac{1}{2}\widehat{CO'O}\Rightarrow2\widehat{IO'O}=\widehat{CO'O}\)
Ta lại thấy: OI là tia phân giác của BOO' (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IOO'}=\frac{1}{2}\widehat{BOO'}\Rightarrow2\widehat{IOO'}=\widehat{BOO'}\)
Xét tứ giác O'CBO có:
\(\widehat{O'CB}+\widehat{CBO}+\widehat{B\text{OO}'}+\widehat{\text{OO}'C}=360^0\)(tổng 4 góc của tứ giác)
Hay \(90^0+90^0+2\widehat{IO'O}+2\widehat{IOO'}=360^0\)
=> \(2\left(\widehat{IO'O}+\widehat{IOO'}\right)=360^0-90^0-90^0=180^0\)
=> \(\widehat{IO'O}+\widehat{IOO'}=\frac{180^0}{2}=90^0\)\
Xét tam giác O'IO có:
\(\widehat{IO'O}+\widehat{IOO'}+\widehat{O'IO}=180^0\)(Tổng ba góc trong tam giác)
Hay \(90^0+\widehat{\text{OIO}'}=180^0\)
=> \(\widehat{\text{OIO}'}=180^0-90^0=90^0\)
Vậy góc OIO' = 90o
c) Xét tam giác O'IO vuông tại I có:
Đường cao IA
Theo hệ thức lượng trong tam giác:
Ta có: IA2 = OA * O'A
hay IA2 = 4 * 9
=> IA = 6 (cm)
Mà IA = IC = IB = 6 (cm)
=> IC + IB = BC
hay BC = 6 + 6 = 12 (cm)
Vậy BC = 12cm
TD
19 tháng 5 2019
a) Xét tứ giác OBIA có OBI=90 (BC là tiếp tuyến của (O))
OAI=90(AI------------------------------)
<=>OBI+OAI=180
<=>tứ giác OBIA nội tiếp
+)cmtt có :tứ giác ICO'A nội tiếp
30 tháng 5 2021
a) Theo tính chất hai tiếp tuyến cắt nhau ta có IA = IB = IC.
Do đó tam giác ABC vuông tại A.
Lại có \(IO_1\perp AB;IO_2\perp AC\) nên tam giác \(IO_1O_2\) vuông tại I.
b) Đầu tiên ta chứng minh kết quả sau: Cho hai đường tròn (D; R), (E; r) tiếp xúc với nhau tại A. Tiếp tuyến chung BC (B thuộc (D), C thuộc (E)). Khi đó \(BC=2\sqrt{Rr}\).
Thật vậy, kẻ EH vuông góc với BD tại H. Ta có \(DH=\left|R-r\right|;DE=R+r\) nên \(BC=EH=\sqrt{DE^2-DH^2}=2\sqrt{Rr}\).
Trở lại bài toán: Giả sử (O; R) tiếp xúc với BC tại M.
Theo kết quả trên ta có \(BM=2\sqrt{R_1R};CM=2\sqrt{RR_2};BC=2\sqrt{R_1R_2}\).
Do \(BM+CM=BC\Rightarrow\sqrt{R_1R}+\sqrt{R_2R}=\sqrt{R_1R_2}\Rightarrow\dfrac{1}{\sqrt{R}}=\dfrac{1}{\sqrt{R_1}}+\dfrac{1}{\sqrt{R_2}}\).
P/s: Hình như bạn nhầm đề
CM
5 tháng 4 2021
K CHO MK VỚI Ạ
HÌNH TỰ VẼ,PHẦN 1 TỰ LÀM
2, Theo tính chất hai tiếp tuyến cắt nhau ta có:
\(IA=IB=IC\)
ΔABC có đường trung tuyến \(AI=\frac{1}{2}BC\)
NÊN: ΔABC VUÔNG TẠI A
⇒ˆBAC=90 độ(dpcm)
3,Theo tính chất hai tiếp tuyến cắt nhau ta có:
\(IO=IO'\)là các tia phân giác của hai góc kề bù \(AIB,AIC\)NÊN:
4,ΔOIO' vuông tại A có:
IA là đường cao nên theo hệ thức giữa cạnh và đường cao:
\(IA^2=OA.OA'\)
\(=9.4=36\)
=>\(IA=6\)
Vậy \(BC=2.IA=2.6=12\left(cm\right)\)
CM
1 tháng 10 2019
a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
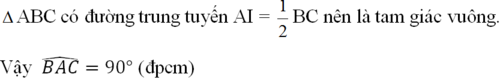
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
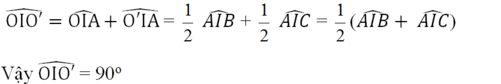
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
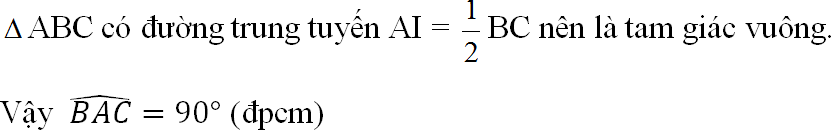
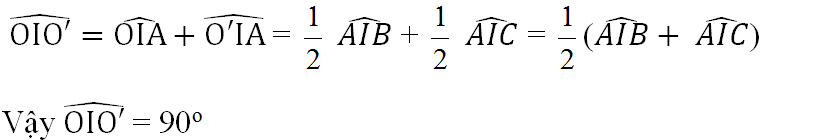
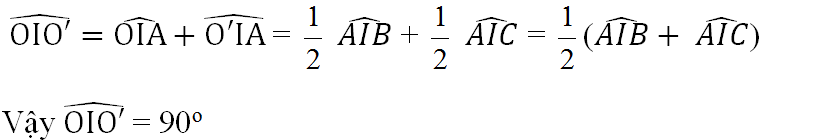
a: Xét (O) có
IB,IA là tiếp tuyến
=>IB=IA và IO là phân giác của góc BIA(1)
Xét (O') có
IA,IC là tiếp tuyến
=>IA=IC và IO' là phân giác của góc AIC(2)
=>IB=IA=IC
b: Xét ΔABC có
AI là trung tuyến
AI=BC/2
=>ΔABC vuông tại A
c: Từ (1), (2) suy ra góc OIO'=1/2*góc BIC=90 độ