Mọi người cho mình hỏi kiểu mệnh đề P=>Q chỉ sai khi P đúng Q sai.
Vậy thì khi P sai Q đúng thì mệnh đề P=>Q có đúng không ạ? Cảm mơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a)
+) Mệnh đề R: “Nếu ABC là tam giác đều thì nó có hai góc bằng \({60^o}\)” có dạng \(P \Rightarrow Q\), với
P: “ABC là tam giác đều” và Q: “Tam giác ABC có hai góc bằng \({60^o}\)”
Ta thấy khi P đúng thì Q cũng đúng. Do đó \(P \Rightarrow Q\) đúng hay R đúng.
+) Mệnh đề T: “Nếu \(a = 2\) thì \({a^2} - 4 = 0\)” có dạng \(P \Rightarrow Q\), với:
P: “\(a = 2\)” và Q: “\({a^2} - 4 = 0\)”.
Ta thấy khi P đúng thì Q cũng đúng. Do đó \(P \Rightarrow Q\) đúng hay T đúng.
b) Mệnh đề \(Q \Rightarrow P\) của hai mệnh đề trên là:
“Nếu ABC có hai góc bằng \({60^o}\) thì nó là tam giác đều”, đúng.
“Nếu \({a^2} - 4 = 0\) thì \(a = 2\)” sai (vì thiếu nghiệm \(a = - 2\)).
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a)
(1) “Nếu ABC là tam giác đều thì nó là tam giác cân” là mệnh đề đúng.
(2) “Nếu 2a – 4 >0 thì a > 2” là mệnh đề đúng.
b) Trong mệnh đề (1) “Nếu ABC là tam giác đều thì nó là tam giác cân”
P: “ABC là tam giác đều”
Q: “ABC là tam giác cân”
Trong mệnh đề (2) “Nếu 2a – 4 > 0 thì a > 2”
P: “2a – 4 > 0”
Q: “a > 2”
Chú ý
Từ “nó” trong mênh đề (1) được hiểu là “ABC”. Do đó khi chỉ ra mệnh đề Q, ta dùng “ABC” thay cho “nó” để mệnh đề được rõ nghĩa.
CM
9 tháng 2 2017
a) Xét P(n) : “3n < n + 100”:
+ Với n = 1, P(1) trở thành: “31 < 1 + 100”. Mệnh đề đúng vì 31 = 3 < 1 + 100 = 101.
+ Với n = 2, P(2) trở thành: “32 < 2 + 100”. Mệnh đề đúng vì 32 = 9 < 2 + 100.
+ Với n = 3, P(3) trở thành: “33 < 3 + 100”. Mệnh đề đúng vì 33 = 27 < 3 + 100.
+ Với n = 4, P(4) trở thành: “34 < 4 + 100”. Mệnh đề đúng vì 34 = 81 < 4 + 100.
+ Với n = 5, P(5) trở thành: “35 < 5 + 100”. Mệnh đề sai vì 35 = 243 > 5 + 100.
Xét Q(n): “2n > n”.
+ Với n = 1, Q(1) trở thành: “21 > 1”. Mệnh đề đúng vì 21 = 2 > 1.
+ Với n = 2, Q(2) trở thành: “22 > 2”. Mệnh đề đúng vì 22 = 4 > 2.
+ Với n = 3, Q(3) trở thành: “23 > 3”. Mệnh đề đúng vì 23 = 8 > 3.
+ Với n = 4, Q(4) trở thành: “24 > 4”. Mệnh đề đúng vì 24 = 16 > 4.
+ Với n = 5, Q(5) trở thành: “25 > 5”. Mệnh đề đúng vì 25 = 32 > 5.
b)
+ Nhận thấy P(n) không đúng với mọi n ∈ N* (sai với n = 5).
+ Với mọi n ∈ N*, Q(n) luôn đúng.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
P: “tam giác ABC vuông tại A”
Q: “tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”
+) Mệnh đề \(Q \Rightarrow P\) là “Nếu tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)thì tam giác ABC vuông tại A”
+) Từ định lí Pytago, ta có:
Tam giác ABC vuông tại A thì \(A{B^2} + A{C^2} = B{C^2}\)
Và: Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) thì vuông tại A.
Do vậy, hai mệnh đề “\(P \Rightarrow Q\)” và “\(Q \Rightarrow P\)” đều đúng.
25 tháng 4 2017
Hướng dẫn trả lời:
Chọn C vì:
Mệnh đề I sai vì không có căn bậc hai của số âm
Mệnh đề IV sai vì √100 = 10 (căn bậc hai số học)
Các mệnh đề II và III đúng
CM
20 tháng 7 2019
Đáp án C
Mệnh đề đúng P ⇔ Q có thể được phát biểu theo các ngôn ngữ khi và chỉ khi, nếu và chỉ nếu, điều kiện cần và đủ nên đáp án C là sai.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
+) Mệnh đề \(P \Rightarrow Q\) là: “Vì tam giác ABC đều nên tam giác ABC cân và có một góc bằng \({60^o}\)”.
+) Mệnh đề \(Q \Rightarrow P\) là: “Tam giác ABC cân và có một góc bằng \({60^o}\) suy ra tam giác ABC đều”.
Dễ thấy cả hai mệnh đề trên đều đúng.
+) Mệnh đề tương đương: (dùng một trong các cách sau:)
“Tam giác ABC đều tương đương tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều là điều kiện cần và đủ để có tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều khi và chỉ khi tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều nếu và chỉ nếu tam giác ABC cân và có một góc bằng \({60^o}\)”
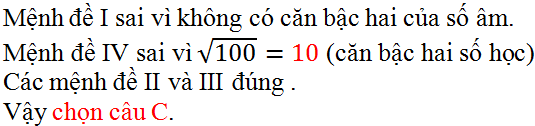
Khi P sai và Q đúng, mệnh đề P=>Q được coi là đúng.