(2x4-3x3-3x2-2+6x) : x2-2 mn giup mk gjai voi nhung cu the chut nha <3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{2x^4-4x^2-3x^3+6x+x^2-2}{x^2-2}=2x^2-3x+1\)

a) \(\left(2x^4-3x^3-3x^2-2+6x\right):\left(x^2-2\right)=2\left(x^2-\dfrac{3}{2}x+\dfrac{1}{2}\right)\left(x^2-2\right):\left(x^2-2\right)=2x^2-3x+1\)


2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
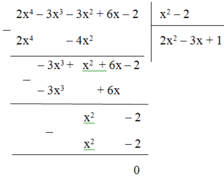
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.

Bài 1:
a) \(3x^2\left(2x^3-x+5\right)-6x^5-3x^3+10x^2\)
\(=6x^5-3x^3+10x^2-6x^5-3x^3+10x^2\)
\(=10x^2+10x^2\)
\(=20x^2\)
b) \(-2x\left(x^3-3x^2-x+11\right)-2x^4+3x^3+2x^2-22x\)
\(=-2x^4+6x^3+2x^2-22x-2x^4+3x^3+2x^2-22x\)
\(=-4x^4+9x^3+4x^2-44x\)

F(x) = 2x5 + 3x3 - 4x4 + 5x - x2 + x3 + x1
F(x) = 2x5 -4x4 + ( 3x3 + x3 ) -x2 + ( 5x+x)
F(x) = 2x5 - 4x4 + 4x3 - x2 + 6x
G(x) = -x2 - x5 + 2x4 - 3x3 + x4 +7
G(x) = -x5 + ( 2x4 + x4) -x2 +7
G ( x) = -x5 + 3x4 -x2 +7
a,F(x)= 2x\(^5\) + 3x\(^3\) - 4x\(^4\) + 5x - x\(^2\) + x\(^3\) + x\(^1\)
=2x\(^5\)- 4x\(^4\) \(+4x^3\)\(-x^2+6x\)
G(x)= -x\(^2\) - x\(^5\) + 2x\(^4\) - 3x\(^3\) + x\(^4\) + 7
=\(-x^5\)\(+3x^4\)\(-3x^3\)\(-x^2\)+7
b,F(x)-G(x)=(2x\(^5\)- 4x\(^4\) \(+4x^3\)\(-x^2+6x\))-\((-x^5+3x^4-3x^3-x^2+7)\)
=\(2x^5-4x^4+4x^3-x^2+6x\) \(+x^5-3x^4\)\(+3x^3\)\(+x^2-7\)
=\(\left(2x^5+x^5\right)\)+\(\left(-4x^4-3x^4\right)\)+\(\left(4x^3+3x^3\right)\)\(\left(-x^2+x^2\right)\)+6x-7
=\(3x^5-7x^4\)\(+7x^3+6x-7\)

a: \(\dfrac{2x^4-3x^3+4x^2+1}{x^2-1}=\dfrac{2x^4-2x^2-3x^3+3x+6x^2-6-3x+7}{x^2-1}\)
\(=2x^2-3x+6+\dfrac{-3x+7}{x^2-1}\)
Để dư bằng 0 thì -3x+7=0
=>x=7/3
b: \(\dfrac{x^5+2x^4+3x^2+x-3}{x^2+1}\)
\(=\dfrac{x^5+x^3+2x^4+2x^2-x^3-x+x^2+1+2x-4}{x^2+1}\)
\(=x^3+2x^2-x+1+\dfrac{2x-4}{x^2+1}\)
Để đư bằng 0 thì 2x-4=0
=>x=2

a) \(...=P\left(x\right)=2x^4-x^4+3x^3+4x^2-3x^2+3x-x+3\)
\(P\left(x\right)=x^4+3x^3+x^2+2x+3\)
\(...=Q\left(x\right)=x^4+x^3+3x^2-x^2+4x+4-2\)
\(Q\left(x\right)=x^4+x^3+2x^2+4x+2\)
b) \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)+\left(x^4+x^3+2x^2+4x+2\right)\)
\(\Rightarrow P\left(x\right)+Q\left(x\right)=2x^4+4x^3+3x^2+6x+5\)
\(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)-\left(x^4+x^3+2x^2+4x+2\right)\)
\(\)\(\Rightarrow P\left(x\right)-Q\left(x\right)=x^4+3x^3+x^2+2x+3-x^4-x^3-2x^2-4x-2\)
\(\Rightarrow P\left(x\right)-Q\left(x\right)=2x^3-x^2-2x+1\)