tìm x
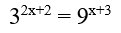
chi tiết nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2016
Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có: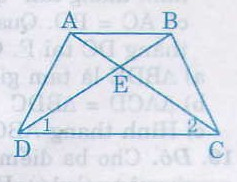 
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
9 tháng 9 2016
Chứng Minh;
Xét tam giác ADC và BCD, có:
AD = BC ( gt )
DC là cạnh chung
AC = BD ( gt )
\(\Rightarrow\)Tam giác ADC = BCD ( c.c.c )
\(\Rightarrow\)Â1 = B1 ( 2 góc Tương ứng )
Mà Góc DAB= CBA ( gt )
\(\Rightarrow\)Â2= B2 ( gt )
\(\Rightarrow\)Tam giác AEB cân tại E
nên EA=EB
mà AC=BD
\(\Rightarrow\)EC=ED A B D C 1 2 2 1 E
AH
Akai Haruma
Giáo viên
23 tháng 7 2023
Lời giải:
$3^{2x+2}=9^{x+3}$
$3^{2x+2}=(3^2)^{x+3}=3^{2(x+3)}=3^{2x+6}$
$\Rightarrow 2x+2=2x+6$
$\Rightarrow 2=6$ (vô lý)
Vậy không có x thỏa mãn đề.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
7 tháng 4 2023
a x 4 - 7,5 = a:4 + 7,5
a x 4 - a x 1/4 = 7,5 + 7,5
a x (4 - 1/4)= 15
a x 15/4 = 15
a= 15 : 15/4
a= 4
24 tháng 9 2018
1 + 1 = 2
bài kiểm tra toán 1 tiết tuần thứ 3 (tiết 16) tùy vào từng trường mà ra đề, ít có trường nào giống nhau lắm nên bạn thông cảm mik thật sự ko biết
GN
5
2 tháng 1 2022
\(\left|x\right|=\dfrac{3}{8}\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{8}\\x=\dfrac{3}{8}\end{matrix}\right.\)
LD
2 tháng 1 2022
|x|=\(\dfrac{3}{8}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{8}\\x=\dfrac{-3}{8}\end{matrix}\right.\)
Vậy x∈{\(\dfrac{3}{8}\);\(\dfrac{-3}{8}\)}
\(3^{2x+2}=9^{x+3}\)
\(\Rightarrow3^{2x+2}=\left(3^2\right)^{x+3}\)
\(\Rightarrow3^{2x+2}=3^{2x+6}\)
\(\Rightarrow2x+3=2x+6\)
\(\Rightarrow2x-2x=6-3\)
\(\Rightarrow0=3\) (vô lý)
Vậy không có x phù hợp