Xét các phân thức \(P = \dfrac{{{x^2}y}}{{x{y^2}}}\), \(Q = \dfrac{x}{y}\), \(R = \dfrac{{{x^2} + xy}}{{xy + {y^2}}}\) .
a) Các phân thức trên có bằng nhau không? Tại sao?
b) Có thể biến đổi như thế nào nếu chuyển \(Q\) thành \(P\) và \(R\) thành \(Q\).


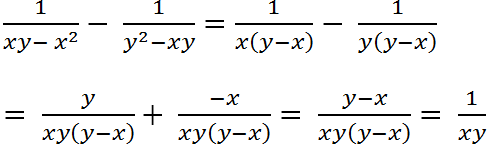
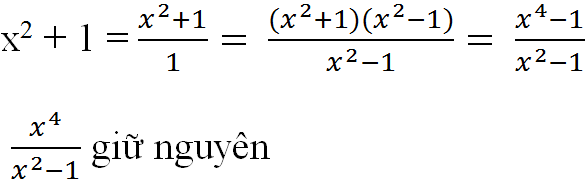
`a, P = x/y`.
`Q = x/y`
`R = (x(x+y))/(y(x+y)) = x/y`
Vậy `3` phân thức bằng nhau.
`b, Q . x/y = R`.
`R : x/y = Q.`