Tính thể tích của một chiếc hộp bánh ít có dạng hình chóp tứ giác đều, có độ dài cạnh đáy là 3cm và chiều cao là \(2,5\)cm.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))

\(V_{chóp.tứ.giác.đêu}=\dfrac{1}{3}.S_{đáy}.h\\ \Leftrightarrow400=\dfrac{1}{3}.a^2.h=\dfrac{1}{3}.10^2.h\\ \Leftrightarrow h=\dfrac{400\times3}{10^2}=12\left(mm\right)\)

Thể tích của hình chóp đều là:
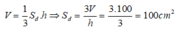
Gọi độ dài cạnh đáy là a.
Do đáy là tam giác đều nên diện tích đáy là:
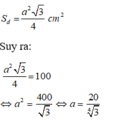
Chọn đáp án D
Diện tích đáy là: \(3.3 = 9\) (\(c{m^2}\))
Thể tích của hình chiếc hộp bánh là: \(\frac{1}{3}.9.2,5 = 7,5\) (\(c{m^3}\))