70. Tam giác ABC có \(\widehat{B}=75^o;\widehat{C}=60^o.\)Kéo dài BC một đoạn CD sao cho \(CD=\frac{1}{2}BC.\)Tính \(\widehat{ADB}\)
Giải nhanh cho tick
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
QT
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\( \Rightarrow R = \dfrac{a}{{2\sin A}};\;\;b = \dfrac{{a.\sin B}}{{\sin A}}\)
Mà \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\)
\( \Rightarrow R = \dfrac{{10}}{{2\sin {{45}^o}}} = 5\sqrt 2 ;\;\;b = \dfrac{{a.\sin {{70}^o}}}{{\sin {{45}^o}}} \approx 13,29\)
Mặt khác: \(\widehat A = {45^o},\widehat B = {70^o} \Rightarrow \widehat C = {65^o}\)
Từ định lí sin ta suy ra: \(c = \dfrac{{a.\sin C}}{{\sin A}} = \dfrac{{10.\sin {{65}^o}}}{{\sin {{45}^o}}} \approx 12,82.\)
Vậy \(R = 5\sqrt 2 ;\;\;b \approx 13,29\); \(c \approx 12,82.\)
QT
1
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Ta có: \(\widehat B = {75^o},\widehat C = {45^o}\)\( \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8\)
Vậy độ dài cạnh AB là 40,8.
27 tháng 9 2021
Ta có \(\widehat{A}+\widehat{ABC}+\widehat{C}=180^0\Rightarrow180^0-3\widehat{C}+\widehat{C}=180^0-70^0=110^0\)
\(\Rightarrow2\widehat{C}=70^0\Rightarrow\widehat{C}=35^0\Rightarrow\widehat{A}=180^0-3\cdot35^0=75^0\)
Ta có BE là p/g nên \(\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{ABC}=35^0\)
Mà \(ED//BC\) nên \(\widehat{B_2}=\widehat{E_2}=35^0\left(so.le.trong\right)\left(1\right)\)
Ta có \(ED//BC\Rightarrow\widehat{E_1}=\widehat{C}=35^0\left(đồng.vị\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\widehat{E_1}=\widehat{E_2}\left(=35^0\right)\)
Vậy ...
24 tháng 11 2018
A B C 4 cm 70 50 x y
HÌNH CHUẨN 100% MK DÙNG THƯỚC VÀ THƯỚC ĐO GÓC ĐỂ ĐO ĐÓ
(ĐO TRÊN MÀN HÌNH MÁY TÍNH)
Cách vẽ
Do góc B=70o, góc A=50o nên góc C=60o
B1: vễ đoạn thẳng BC dài 4 cm
B2: Từ B kẻ tia Bx sao cho góc B=70o
từ C kẻ tia Cy sao cho góc C=60o
Tia Bx, Cy cắt nhau tại A, ta đc tam giác ABC thỏa mãn đề bài
TK MK NHA BN
***** CHÚC BẠN HỌC GIỎI*****
24 tháng 11 2018
Cách vẽ:
B1: Vẽ góc xÂy = 50*
B2: Trên Ax lấy điểm B, sau đó vẽ góc B = 70* kéo dài cắt Ay tại C
=> Ta có tam giác ABC thỏa mãn
10 tháng 12 2016
B A C y x
- Vẽ đoạn thẳng \(BC=2cm\)
- Trên cùng một nửa mặt phẳng bờ \(BC\) , vẽ các tia \(Bx\) và \(Ay\) sao cho \(\widehat{ABx}=70^0\) ; \(\widehat{BAy}=50^0\)
****** Hình vẽ chỉ mang tính chất minh học thôi bạn nhé !!!!!!!!!
17 tháng 9 2023
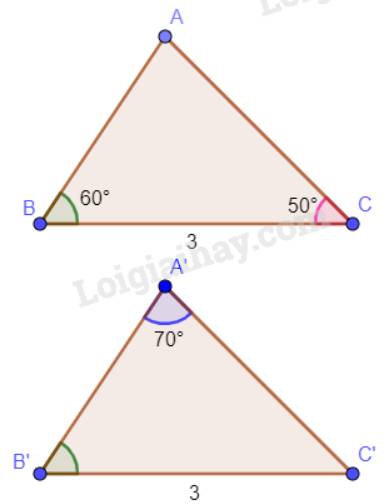
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
WR
19 tháng 8 2017
A B C M
Th1: AB<AC (hình hơi lệch chuẩn chút :P)
giá sử đường thẳng qua đỉnh A chia tam giác ABC thành hai tam giác cân ABM cân tại A và ACM cân tại M
khi đó (ko viết mũ góc tự hiểu ha)
=> B=M
Lại có M=C+MAC=2C
=>B=2C, lại có A=75
=>B=70
C=35
T.tự Th AC<AB
còn AB=AC=>B=C=52,5
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
A B C D F
Từ đỉnh B của \(\Delta\)ABC hạ đường cao BF, nối F với D.
Có \(\Delta\)BFC vuông tại F, ^FBC=900-^ACB=900-600=300 \(\Rightarrow\)FC=1/2BC (Tính chất của tam giác vuông có góc 300)
Mà CD=1/2BC \(\Rightarrow\)CD=FC\(\Rightarrow\Delta\)FCD cân tại C. Lại có: ^FCD=1800-^ACB=1800-600=1200.
\(\Rightarrow\)^CFD=^CDF=300. Ngoài ra: ^FBC=300 \(\Rightarrow\)^CDF=^FBC=300\(\Rightarrow\Delta\)BFD cân tại F\(\Rightarrow\)FB=FD (1)
Tính được: ^FBA=^ABC-^FBC=750-300=450. Mà ^BAC=1800-(^ABC+^ACB)=450\(\Rightarrow\)^FBA=^FAB=450
\(\Rightarrow\Delta\)AFB vuông cân tại F \(\Rightarrow\)FB=FA (2).
Từ (1) và (2) \(\Rightarrow\)FD=FA \(\Rightarrow\Delta\)AFD cân tại F. Ta thấy ^AFD kề bù với ^CFD \(\Rightarrow\)^AFD=1800-^CFD=1500.
\(\Rightarrow\)^FAD=^FDA=150 \(\Rightarrow\)^ADB=^FDA+^CDF=150+300=450.
Vậy ^ADB=450.