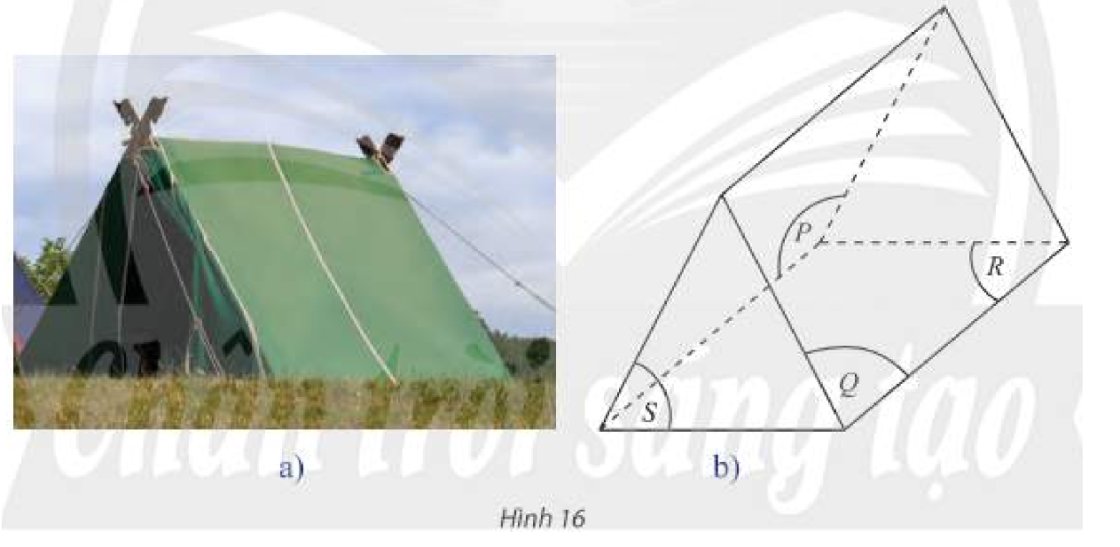
Một chiếc lều (Hình 16a) được minh hoạ như Hình 16b.
a) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến song song.
b) Tìm ba mặt phẳng cắt nhau từng đôi một theo ba giao tuyến đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I = d1 ∩ d2; (P) là mặt phẳng chứa (d1) và (d2).
Gọi d3 ∩ d1 = M; d3 ∩ d2 = N.
+ M ∈ d1, mà d1 ⊂ (P) ⇒ M ∈ (P)
+ N ∈ d2, mà d2 ⊂ (P) ⇒ N ∈ (P).
Nếu M ≠ N ⇒ d3 có hai điểm M, N cùng thuộc (P)
⇒ d3 ⊂ (P)
⇒ d1; d2; d3 đồng phẳng (trái với giả thiết).
⇒ M ≡ N
⇒ M ≡ N ≡ I
Vậy d1; d2; d3 đồng quy.

– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b

Đáp án C.

Mặt cầu S : x - 1 2 + y - 1 2 + z + 2 2 = 4 có tâm và bán kính R = 2
Xét ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao tuyến là các đường tròn (C1), (C2), (C3 ) lần lượt là
![]()
Gọi r1, r2, r3 lần lượt là bán kính của các đường tròn giao tuyến của mặt cầu (S) với ba mặt phẳng (P1), (P2), (P3 )
Vì (P1), (P2) đi qua tâm I(1;1;-2) nên
![]()
nên
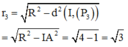
Tổng diện tích của ba hình tròn (P1), (P2), (P3 ) là
![]()

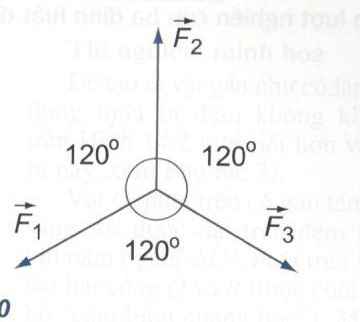
Biểu diễn thành hình sau:
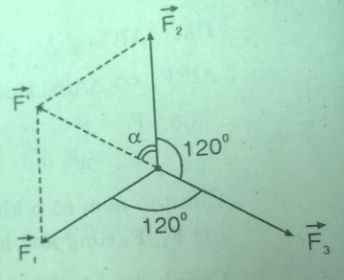
HBH \(OF_1F'F_2\) gồm hai tam giác đều:
\(\Rightarrow F'=F_1=F_2=F_3\) và \(\alpha=60^o\)
Có \(F'vàF_3\) là hai vecto ngược chiều
\(\Rightarrow\overrightarrow{F}=\overrightarrow{F'}+\overrightarrow{F_3}=\overrightarrow{0}\)
a: (P),(Q),(R)
b: (P),(Q),(S)