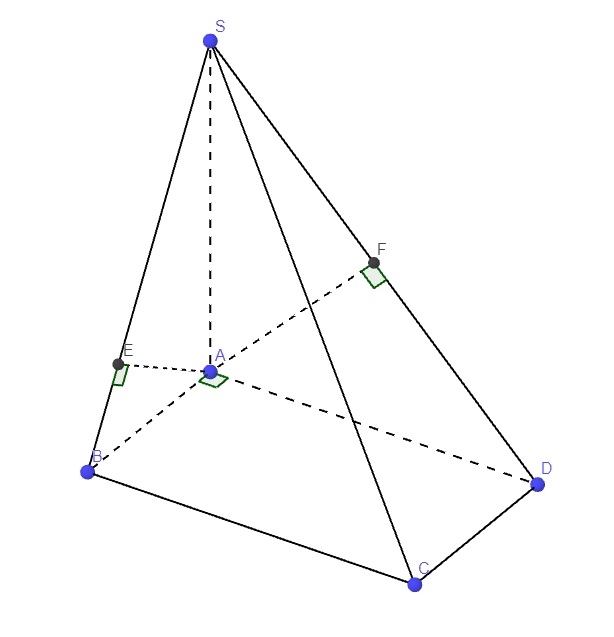
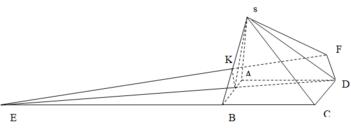
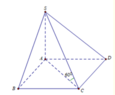
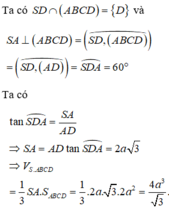Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB=4a, AD=3a. Các cạnh bên đều có độ dài 5a. Tính góc giữa (SBC) và (ABCD) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2023
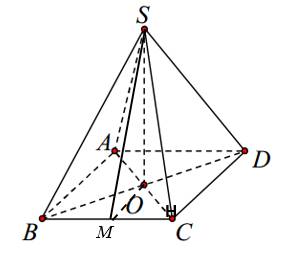
Gọi \(M\) là trung điểm \(BC\).
Ta có:\(OM=\dfrac{1}{2}.AB=2a;AC=\sqrt{AB^2+BC^2}=5a;OC=\dfrac{1}{2}AC=\dfrac{5}{2}a\)
\(SO=\sqrt{SC^2-OC^2}=\dfrac{5\sqrt{3}}{2}a\)
\(\left[S,BC,A\right]=\widehat{SMO}\)
\(\tan\widehat{SMO}=\dfrac{SO}{OM}=\dfrac{5\sqrt{3}}{4}\)
Suy ra:\(\widehat{SMO}=65,2^o\)
\(\Rightarrow D\)
CM
2 tháng 10 2018
Đáp án A
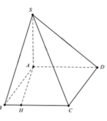
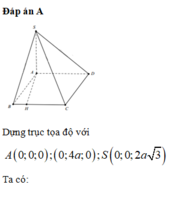
Dựng trục tọa độ với A 0 ; 0 ; 0 ; 0 ; 4 a ; 0 ; S 0 ; 0 ; 2 a 3
Ta có: A H = A B sin 60 0 = 3 a 3 2 ; B H = 3 a 2
Do đó B = 3 a 3 2 ; − 3 a 2 ; 0 ; C 3 a 3 2 ; 5 a 2 ; 0
Khi đó n S B C ¯ = k S B ¯ ; B C ¯ = 4 ; 0 ; 3 ; n S C D ¯ = k S C ¯ ; D C ¯ = 3 ; 3 ; 2 3
Do đó cos S B C ; S C D ^ = 10 3 4 2 + 3 2 24 = 1 2 ⇒ S B C ; S C D ^ = 45 0
CM
9 tháng 7 2017
Đáp án A
Ta có A ⇔ = a 2 + a 2 2 = a 3
S
A
=
A
C
tan
60
0
=
a
3
.
3
=
3
a
;
S
A
B
C
D
a
.
a
2
=
a
2
2
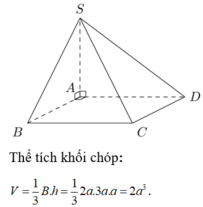
Thể tích hình chóp S.ABCD là:
V = 1 3 S A . S B A C D = 1 3 .3 a . a 2 2 = a 3 2
CM
9 tháng 11 2017
: Đáp án D
Thể tích khối chóp là: V = 1 3 S A . S A B C D = 1 3 a .2 a .3 a = 2 a 3 .
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Lần lượt kẻ \(AE\perp SB\) (1) và \(AF\perp SD\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AE\) (2)
(1);(2) \(\Rightarrow AE\perp\left(SBC\right)\)
Hoàn toàn tương tự ta có \(AF\perp\left(SCD\right)\)
\(\Rightarrow\) Góc giữa (SBC) và (SCD) là góc giữa AE và AF
Cũng từ \(BC\perp\left(SAB\right)\) mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBCD) và đáy
\(\Rightarrow\widehat{SBA}=60^0\Rightarrow SA=AB.tan60^0=a\sqrt{3}\)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AF=\dfrac{a\sqrt{6}}{2}\)
\(SB=\sqrt{SA^2+AB^2}=2a\) ; \(SD=a\sqrt{6}\)
\(BD=\sqrt{AB^2+AD^2}=2a\Rightarrow cos\widehat{BSD}=\dfrac{SB^2+SD^2-BD^2}{2SB.SD}=\dfrac{\sqrt{6}}{4}\)
\(SE=\sqrt{SA^2-AE^2}=\dfrac{3a}{2}\) ; \(SF=\sqrt{SA^2-AF^2}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow EF=\sqrt{SE^2+SF^2-2SE.SF.cos\widehat{BSD}}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow cos\widehat{EAF}=\dfrac{AE^2+AF^2-EF^2}{2AE.AF}=\dfrac{\sqrt{2}}{4}\)
CM
13 tháng 4 2019
Đáp án B
Kẻ H K ⊥ S B ⇒ H K ⊥ ( S C B ) .
Gọi E = D H ∩ B C , kẻ D F / / H K ( F ∈ E K )
⇒ D F ⊥ ( S B C )
Ta có S H = S A 2 - A H 2 = 2 a .
Xét ∆ S H B có 1 H K 2 = 1 S H 2 + 1 H B 2 = 13 36 a 2
⇒ H K = 6 a 13
Ta có E H E D = H B C D = 3 4 .
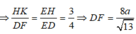
Ta có S D = S H 2 + D H 2 = 2 a 2
