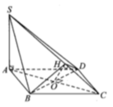
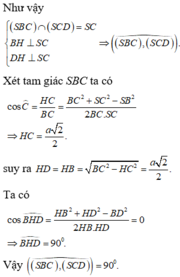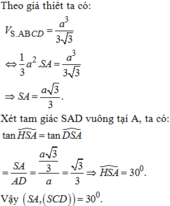Cho chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và (SCD) tạo với mặt phẳng đáy góc 45°. Tính góc giữa (SBC) và (SCD).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)

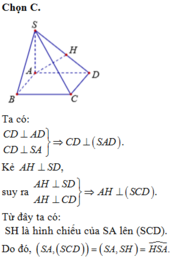
Chọn C.
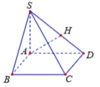
Ta có: 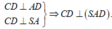
Kẻ AH
⊥
SD, suy ra 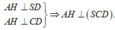
Từ đây ta có: SH là hình chiếu của SA lên (SCD).
Do đó: ![]()
Theo giả thiết ta có:
Xét tam giác SAD vuông tại A, ta có:
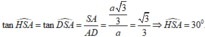
Vậy ![]()

Đáp án A
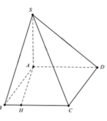
Dựng trục tọa độ với A 0 ; 0 ; 0 ; 0 ; 4 a ; 0 ; S 0 ; 0 ; 2 a 3
Ta có: A H = A B sin 60 0 = 3 a 3 2 ; B H = 3 a 2
Do đó B = 3 a 3 2 ; − 3 a 2 ; 0 ; C 3 a 3 2 ; 5 a 2 ; 0
Khi đó n S B C ¯ = k S B ¯ ; B C ¯ = 4 ; 0 ; 3 ; n S C D ¯ = k S C ¯ ; D C ¯ = 3 ; 3 ; 2 3
Do đó cos S B C ; S C D ^ = 10 3 4 2 + 3 2 24 = 1 2 ⇒ S B C ; S C D ^ = 45 0

Đáp án A
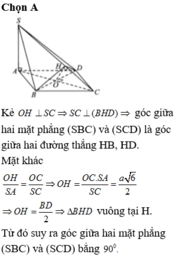
Do AB // CD => giao tuyến của mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AB.
Dễ thấy Sx ⊥ (DSA) => Góc tạo bởi mặt phẳng (SAB) và (SCD) bằng góc D S A ^ = a r c tan 1 3 = 30 0