Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H.4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

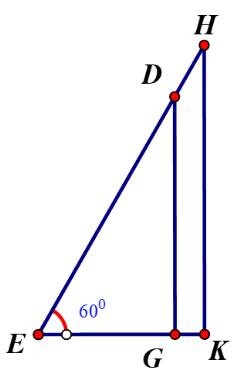
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.

Giả sử khoảng cách từ vị trí đặt đến đầu bên trái là x (m)
Theo điều kiện cân bằng đòn bẩy: \(xP_1=\left(2-x\right)P_2\Leftrightarrow500x=\left(2-x\right)300\Rightarrow x=0,75\left(m\right)\)
Vậy cần đặt gậy vào vị trí cách đầu bên trái 1 khoảng 0,75 m thì nó nằm cân bằng

Vẽ tam giác ABC, BC=2,5m, AC=6,5m. ABC vuông tại B
Dịnh lí Pitago: AB=\(\sqrt{AC^2-BC^2}\) =6m

THAM KHẢO:
Ta coi chân bàn như đường thẳng và mặt bàn, mặt sàn là 2 mặt phẳng.
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn nên hai mặt phẳng đó có song song với nhau vì hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Gọi F B → là hợp lực của lực căng T → và phản lực N B → của sàn. Ta có hệ ba lực cân bằng là P → , N A → và N B → . Ba lực này đồng quy tại C (H.17.6G).
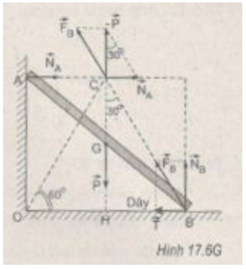
Vì OA = CH = OB 3 /2 nên tam giác OCB là tam giác đều. Từ tam giác lực ta có :
T = NA= Ptan 30 ° = P/ 3

Gọi độ dài của thang là BC, khoảng cách từ chân thang đến chân tường là AC
Theo đề, ta có: BC=3,5m; AC=1,6m; AC\(\perp\)AB tại A
Ta có: ΔABC vuông tại A
=>\(cosC=\dfrac{CA}{CB}\)
=>\(cosC=\dfrac{1.6}{3.5}=\dfrac{16}{35}\)
=>\(\widehat{C}\simeq63^0\)
=>\(60^0< =\widehat{C}< =65^0\)
=>Đạt tiêu chuẩn
Chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn với mép tường tạo thành hai đường thẳng chéo nhau nên không thể song song.