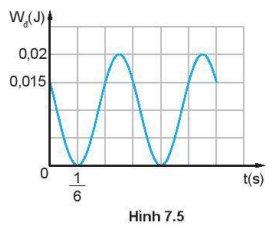
Hình 7.5 là đồ thị động năng theo thời gian của một vật khối lượng 0,4 kg dao động điều hoà. Tại thời điểm ban đầu vật đang chuyển động theo chiều dương, lấy π2 = 10. Viết phương trình dao động của vật.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
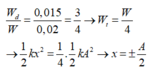
Tại thời điểm ban đầu, vật chuyển động theo chiều dương 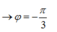
Sau 1 6 ( s ) , vật chuyển động đến vị trí biên, tức là khi đó vật quay được một góc
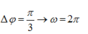
→ 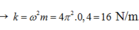
Cơ năng
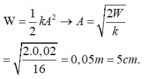
Phương trình dao động của vật là x = 5cos(2πt – π/3) cm.

Đáp án A
+ Từ đồ thị ta thấy : ![]()
+ Dựa vào đáp án suy ra : ![]()
![]()
loại B, D.
+ Do tại thời điểm t = 0 vật chuyển động theo chiều dương nên pha ban đầu của dao động là âm :
![]()

Đáp án A
+ Từ đồ thị ta thấy :
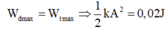
+ Dựa vào đáp án suy ra : ω = 2 π rad/s => k = ω 2 . m = 16 N/m => A = 0,05 m = 5cm => loại B, D.
+ Do tại thời điểm t = 0 vật chuyển động theo chiều dương nên pha ban đầu của dao động là âm : x = 5 cos 2 πt - π 3 cm.
Từ đồ thị ta có:
Tại thời điểm ban đầu t = 0: Wđ = 0,015 J ⇒Wt = 0,02−0,015 = 0,005(J)
⇔\({{\rm{W}}_t} = \frac{{\rm{W}}}{4} \Rightarrow {x_0} = \pm \frac{A}{2}\)
Tại thời điểm t1 = \(\frac{1}{6}\): Wđ = 0 ⇒ x1 = ±A
Dựa vào đồ thị ta suy ra: x0 = \(\frac{A}{2}\); x1 = A
Khoảng thời gian từ x0 đến x1 là: Δt = \(\frac{T}{6}\)⇔T = 1(s) ⇔ ω = \(\frac{{2\pi }}{T} = 2\pi \) (rad/s)
\({{\rm{W}}_{{\rm{dmax}}}} = \frac{1}{2}m{\omega ^2}{A^2} = 0,02 \Leftrightarrow A = \sqrt {\frac{{{{\rm{W}}_{{\rm{dmax}}}}}}{{m{\omega ^2}}}} = \sqrt {\frac{{2.0,02}}{{0,4{{\left( {2\pi } \right)}^2}}}} = 0,05m = 5cm\)
Tại t=0:
\(\left\{ \begin{array}{c}{x_0} = A\cos \varphi = \frac{A}{2}\\v = - A\sin \varphi > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi = \frac{1}{2}\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = - \frac{\pi }{3}\)
Phương trình dao động của vật: x = 5cos(2πt − \(\frac{\pi }{3}\))(cm)