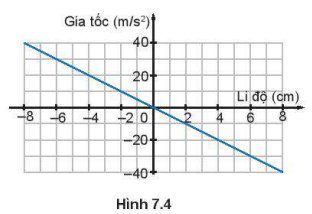
Đồ thị Hình 7.4 mô tả mối liên hệ giữa gia tốc và li độ của một vật dao động điều hoà.
Sử dụng số liệu trong đồ thị Hình 7.4 để tính tần số của dao động.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Biên độ dao động A=0,2 cm
Chu kì T=0,4 s
Tần số \(f = \frac{1}{T} = \frac{1}{{0,4}} = 2,5Hz\)
Tần số góc của dao động \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi rad/s\)
b) Li độ của vật dao động tại các thời điểm t1, t2, t3 ứng với các điểm A, B, C trên đường đồ thị li độ – thời gian lần lượt là x1=-0,1 cm, x2= -0,2 cm, x3= 0 cm.
c) Vì gốc thời gian trùng với vị trí cân bằng nên li độ cũng chính là độ dịch chuyển từ vị trí cân bằng đến vị trí của vật tại các điểm A, B, C.

Đáp án D
Từ đồ thị ta có: v max = 20 π c m / s = ω A ⇒ ω = v max A = 2 π r a d / s ⇒ T = 1 s
W d − max = 200 m J = 0 , 2 J = W = 1 2 k A 2 ⇒ k = 40 N / m 2

Đáp án B
Từ đồ thị thì ta thấy: a max = 200 c m / s 2 và A = 2 c m
⇒ a max = ω 2 A ⇔ 200 = 2 ω 2 ⇒ ω = 10 r a d / s

Chọn đáp án B
Từ đồ thị, ta có a m a x = ω 2 A = 2 m / s 2 và x m a x = A = 2 c m
→ ω = a m a x A = 2 0 , 02 = 10
Ta có: `a_[max]=40(m//s^2)`
Mà `A=8(cm)=0,08(m)`
`=>\omega=\sqrt{[a_[max]]/A}=10\sqrt{5}(rad//s)`
`=>f=[\omega]/[2\pi]=[5\sqrt{5}]/[\pi] (Hz)`